1. Ein Unterrichtsprotokoll aus Mathematik soll zunächst zeigen, wie hilflos ein Lehrer die Kinder sein läßt, wenn er meint, nach einem uniformen methodischen Schema in genormtem Tempo voranschreiten zu müssen.

In einer 6. Schulstufe hat eine Lehrerin während einer Probelektion zum Finden des kleinsten gemeinsamen Vielfachen anzuleiten:

Sie klebt zwölf rote Scheiben ungeordnet an die Tuchtafel und fordert die Kinder auf, sie mögen die Plättchen so ordnen, daß sie leicht und rasch abgezählt werden können. Der Reihe nach werden die sich meldenden Schüler an die Tafel gerufen, und sie legen Zweier-, Dreier-, Vierer- und Sechserreihen. Zur Bestätigung dafür, daß das Teilziel erreicht ist, werden die Reihen im Chor durchgezählt.

"Wenn es mehr Plättchen wären", fährt die Lehrerin fort, "würde die Zahlenreihe noch weitergeführt werden: 14, 16, 18, 21 usw. Wir haben nur 12 Plättchen geordnet. Statt daß wir Gruppen durchzählen wie 2, 4, 6, 8, 10, 12, könnten wir auch sagen 6 x 2 = 12. Wir haben also das Sechsfache von 2 gebildet. Wenn 12 das Sechsfache von zwei ist, was ist denn dann 6? 8? 10?"

Die Kinder stellen sich auf diesen Schematismus ein und melden sich mit den richtigen Antworten.

Die Lehrerin hält an der Tafel schriftlich fest: 4, 6, 8 ... nennen wir Vielfache der Zahl 2.

Sie überträgt das bisherige Ergebnis auf die Dreierreihe: Welches sind nun Vielfache von 3? - Die Kinder sprudeln 6, 9, 12 etc. hervor, und die Lehrerin weist darauf hin, daß es zu jeder Zahl unendlich viele Vielfache gibt.

In verkürzter Form seien die übrigen Anleitungen genannt, mit denen die Lehrerin ihre Schüler von Station zu Station weitergeschoben hat. Ob es Stationen an Denkbahnen waren, die von allen befahren werden konnten, wird noch überprüft werden können.

L: "Wir schreiben uns nun die Vielfachen von 4 und 6 ins Heft." In beiden Reihen werden die gleichen Zahlen (12, 24, 36 etc.) eingeringelt.

L: "Die Vierer- und die Sechserreihe haben also gleiche gemeinsame Vielfache. Welches ist das kleinste gemeinsame Vielfache der beiden Reihen?" Die Kinder nennen 12.

L: "Man schreibt das so: kgV(4,6) = 12."

Die Reihen 8 und 12 werden noch herangezogen und 24 als deren kgV umrandet.

L: "Das geht bei den kleinen Zahlen sehr leicht. Wenn wir aber größere haben, gibt es eine andere einfache Lösung. Wir schreiben die beiden Zahlen nebeneinander auf; rechts von jeder wird ein senkrechter Strich gezogen:

Die Zahl 8 ist ein Vielfaches von 2. Wir teilen nun die Zahl 8 so oft wie möglich durch ihren kleinsten Teiler, nämlich 2.

Mit der Zahl 12 machen wir es ebenso. 3 ist kein Vielfaches von 2 mehr, daher teilen wir durch die nächstgrößere Zahl, die restlos enthalten ist; das ist 3.

"Wir vergleichen nun die senkrechten Zahlenreihen. Die Zahlen einer Reihe schreiben wir nebeneinander; von der zweiten Reihe haken wir alle Zahlen ab, die in der ersten schon vorgekommen sind, und schreiben diejenigen dazu, die übrigbleiben."

Die Ausführungen sind durch saubere Eintragungen ins Tafelbild begleitet worden.

Nun wird diese Methode des Faktorenzerlegens auch am Zahlenpaar 4 und 6 vorexerziert. Dann sagt die Lehrerin: "Bevor wir ein Beispiel gemeinsam rechnen, schreiben wir das Tafelbild ab."

Mittlerweile sind 40 Minuten vergangen. Der anwesende Mentor unterbricht die Lehrerin und wendet sich mit folgender Aufgabe an die Schüler: "Ich sage euch jetzt jeweils zwei Zahlen, die so klein sind, daß man das kleinste gemeinsame Vielfache leicht im Kopf ausrechnen kann. Schreibt also bitte das kleinste gemeinsame Vielfache neben die Zahlen 6 und 8, 8 und 5, 3 und 7."

Von den 25 Kindern haben 8 drei richtige Lösungen erzielt, vier Kinder haben zwei Aufgaben gelöst, 13 haben bei keinem Zahlenpaar das kleinste gemeinsame Vielfache gefunden. Sie haben etwa geschrieben: Von 6 bis 12, von 8 bis 16; oder: 6, 8 = 2. Auch Angaben wie 6 = 1, 8 = 1 sind vorgekommen (Im leiblichen Bereich würde eine vergleichbare Hilflosigkeit spontane Hilfsmaßnahmen hervorrufen; warum sind wir im geistigen so leicht bereit, das Gebrechen zu taxieren und den damit Behafteten abzuurteilen?)

Unser Beispiel ist kein Sonderfall, sondern ist prototypisch für den Frontalunterricht, der in unseren Schulen vorherrscht. Wer genau zusieht, wird nicht der Einbildung erliegen, daß er es mit drei Leistungsniveaus zu tun habe (etwa 8 Erfolgreiche, 4 Labile, 13 Erfolglose), sondern mit einer kontinuierlich ansteigenden bzw. abfallenden Rangreihe, auf der vom frontal unterrichtenden Lehrer eine mutmaßlich "altersgemäße" Schwierigkeitsstufe - in unserem Fall liegt sie knapp oberhalb der Nahtstelle zwischen den Erfolgreichen und den Labilen - angepeilt worden ist. Damit ist er dem Anspruchsniveau einer Zufallsgruppe gerecht geworden. Der größere Rest hat das Schicksal der übermäßigen oder zu geringen Beanspruchung erlitten.

Eine Unterrichtsskizze zur Binnendifferenzierung soll zeigen, wie dieselbe Thematik mit mehr Rücksicht auf die "Verschiedenheit der Köpfe" unterrichtet werden könnte:

Um die Schüler zu motivieren - wenn sie schon nicht von ihren eigenen Problemen ausgehen dürfen - stellt der Lehrer das kleinste gemeinsame Vielfache in den Dienst der Verteilung von Bruchstücken, wobei eine der aus dem Orient überlieferten Erzählungen von geheimnisvoll verschleierten Testamenten den Anlaß zu dieser Verteilung hätte abgeben können (Person A bekommt ein Drittel, B ein Viertel, und den Rest erhält derjenige, der die Bruchrechnung lösen kann...).

Einige nehmen den Rechenstift. Andere zeichnen Brüche wie Tortenstücke. Der Lehrer bietet ein Hilfsmittel an, weist aber darauf hin, daß sich diejenigen nicht stören lassen mögen, die bereits einen aussichtsreichen Weg beschritten haben. Er hat eine Scheibe auf Drittel, Viertel und den Rest zerschnitten und hat jeden Teil verschieden gefärbt (damit beim späteren Vergleichen und Messen kein Irrtum entsteht). Dieses Anschauungsmittel hat er in mehreren Auflagen vorbereitet, um jeden neuen Vorschlag auf seine Stichhaltigkeit hantierend überprüfen zu können. "Wenn eine Torte", meint er, "so ungerecht aufgeteilt worden ist, kann man das auf verschiedene Weise korrigieren." Die Schüler - in dieser Szene werden sich vorwiegend die Schwachen um den Lehrer versammelt haben - schlagen vielleicht vor, daß man durch das Abschneiden entsprechender Teile vom jeweils größeren Stück die kleineren auffüllen und schließlich mit der Waage Gerechtigkeiten herstellen könnte...Der Lehrer ist durchaus einverstanden, aber er möchte einen mathematisch sauberen Weg gehen, eine das Probieren überholende, berechenbare Lösung wissen. Die Anregung geht an alle, anerkennend auch diejenigen, die sich von vornherein auf einen rechnerischen Weg besonnen haben.

Das Zerteilen der Einzelstücke auf völlig gleiche Elemente wird vorgeschlagen (ob von einem Schüler oder letztlich doch vom Lehrer, läßt sich nicht vorplanen). Schließlich sind die einzelnen Teile der Scheibe in deren Zwölftel zerschnitten und lassen sich nicht nur "definieren", sondern auch gerecht dreiteilen.

In sokratischer Ironie führt der Lehrer zu einigen "Nachdenklichkeiten", die das Durchschauen der Zusammenhänge fördern sollen: "Daß zu Dritteln und Vierteln die Zwölftel passen, muß doch ein eigenartiger Zufall sein...!?" "Wäre es nicht günstig, die Stücke nochmals zu zerschneiden; vielleicht würde die Lösung noch genauer werden?"

Die gewonnene Erkenntnis wird gleichsam zu ihrer Sicherung in verschiedenen Formulierungen verbalisiert und über diesen sprachlichen Zugriff endgültig begriffen: Ungleiche Bruchstücke kann man gleichmachen oder auch nur ermessen, indem man sie mehrfach bzw. vielfach zerkleinert; diese Zerkleinerung muß man so lange fortsetzen, bis die einzelnen Stücke einander genau gleichen; die Zerkleinerung der Bruchstücke kommt einer Vergrößerung der Nenner der Bruchzahl gleich; die Zahlen, die im Nenner der Brüche stehen, werden auf ein gemeinsames Vielfaches multipliziert; zwölf ist ein Vielfaches von 3 und 4; 12 wäre auch ein Vielfaches von 2 und 6; ein noch größeres Vielfaches (24,48) könnte auch herangezogen werden, aber es wäre ein unnützer Aufwand, eine unökonomische Vorgangsweise; es ist klar, daß bei diesem Erweitern auch die Zähler multipliziert werden müssen, sonst würde der Wert des Bruchs verändert werden...

Nun gibt der Lehrer weitere Zahlenpaare vor, die auf ihr kgV erweitert werden sollten (bzw. für die ein gemeinsamer Nenner zu suchen wäre, wenn sie in Bruchzahlen verwendet würden): 3,8; 4,6; 5,12; 8,14 etc. bis zu relativ komplexen Paaren wie 28,36; 82,95 u.a. Arbeitsblätter bzw. Arbeitsbücher werden um so fruchtbringender einsetzbar sein, je mehr sie im Sinne der Assignments der Helen Parkhurst neben der Aufgabenstellung auch methodische Hinweise enthalten. Der Lehrer gibt die Anregung: "Sobald ihr an die Grenze eures Könnens gelangt seid, besprecht ihr euch mit dem Nachbarn (Partner). Wenn ihr dann ein wenig an die Multiplikationen denkt, die hinter den meisten Zahlen stecken, wird euch das nützlich sein!" - Diejenigen, die das Prinzip bereits durchschaut haben, werden nun einen Großteil der Aufgaben ohne Lehrerhilfe lösen können. Der Lehrer selbst geht zu den einzelnen Schülern und beobachtet ihren Fortschritt. Bei denen, die nicht zu Rande kommen, schreibt er ein "L" neben die Aufgabe (oder welche Konvention er sonst wählt). "Lehrer heißt das", sagt er jedem, soweit er das Zeichen noch nicht kennt, "und bedeutet, daß ich dir gleich helfen werde." (Ich werde dir helfen, ist merklich weniger frustrationsbesetzt - wenn überhaupt - als jede negative Zensur und jedes Minus neben der Testaufgabe.) Dann ruft er das mehr oder weniger große Häuflein der Schüler, deren kognitive Landkarte noch blind geblieben ist, zu sich an die Tafel. Er durchstöbert seinen Fundus an Lernstrategien, um auch ihnen die Einsicht zu vermitteln.

Er legt Pappkartonkärtchen mit den Zahlen 1-20 in einer Reihe auf den Boden. Dann stellt sich eine Gruppe von Schülern mit der Zweierreihe dahinter.

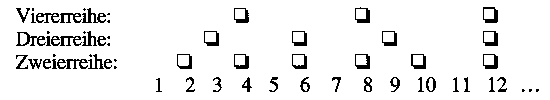
Die veranschaulichten Zahlenverhältnisse werden in "Redewendungen" in die "Veranstrengung des Begriffes" genommen: 6 kommt in der Zweierreihe vor und auch in der Dreierreihe; 12 kommt in der Zweier-, Dreier-, Vierer- und Sechserreihe vor; 6 ist ein Vielfaches von 2 und 3; 12 ist ein Vielfaches von 2, 3, 4 und 6; 6 und 12 sind gemeinsame Vielfache von 2 und 3.

Der Lehrer schreibt die Zahlenreihe 1 bis n an die Tafel. Mit verschiedenen Farbkreiden zieht er rhythmische Wellenlinien, die die Einmaleinsreihen symbolisieren:

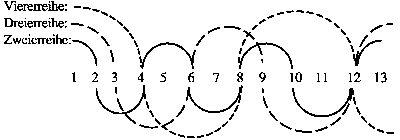
Wiederum setzt die sprachliche Formulierung den Schlußpunkt zur gedanklichen Bewältigung.

Es darf vermutet werden, daß sich ein Teil der Schüler bereits nach der ersten "verselbständigt" und nach der zweiten auch der Rest das Grundprinzip durchschaut hat. Alle arbeiten nun individuell an ihren Aufgaben; die einen bereits im Sinn einer geistigen Gratwanderung, die anderen gleichsam noch im ersten Aufstieg.

Skeptiker werden einwenden, daß die Langsamen oder sonstwie Behinderten die Schnellen und besonders Tüchtigen nie einholen können, daß sie also nie "auf gleich" kommen werden. - Das war aber auch nie das der Schule vorgegebene Ziel - und wenn sie es sich je selbst gestellt hat oder noch stellen sollte, dann müßte sie sich schleunigst eingestehen, daß sie es nie erreicht (hat). Der große Unterschied zwischen einer Pädagogik, die Homogenität anstrebt, und der, die um die unaufhebbare Heterogenität weiß, ist der, daß die eine inhumane (eliminierende) Maßnahmen setzen muß, während die andere die Differenzen bejaht und mit ihnen zu leben weiß. Sie versucht, jedem das Seine zu geben. (Diese Pädagogik hat gleichsam den Schritt zur reiferen Moral schon getan: Nicht jedem das Gleiche ist ihre Maxime, sondern jedem das Seine!)

Die letzte Phase dieses Unterrichtsablaufes gehört denen, die sich über die Faktorenzerlegung Gedanken gemacht haben. Ob jeder Schwache diesen Schritt noch mitvollzieht oder nicht, macht wenig aus. Wenn er den Sinn der Operation als solchen erfaßt hat, wird er mit den für ihn unauflösbaren Zahlenpaaren zu begabten Freunden gehen. (Das Problem erkannt und die Lösungsstrategie durchschaut zu haben, ist wichtig; zu Detailaufgaben mögen Spezialisten herangezogen werden.)

Die früh in die Still- bzw. Partnerarbeit entlassenen Schüler werden ihre Hypothesen darstellen. Haben sie selbst die Lösung bzw. einen Algorithmus gefunden, wird sie der Lehrer bei dessen Interpretation unterstützen. Ist dies nicht der Fall, greift er ihnen mit folgender Analyse unter die Arme: "Daß das Multiplizieren von zwei Zahlen ein Vielfaches ergibt, haben wir eingesehen. Aber dieses Vielfache ist in den meisten Fällen nicht das kleinste, und daher ist der Umgang mit ihm sehr aufwendig. Nehmen wir einmal das kleinste gemeinsame Vielfache von Zahlen, bei denen wir es noch 'im Kopf' finden: 12, 9, 18; kgV = 36. Betrachten wir die Faktoren, aus denen jede der drei Zahlen wie auch ihr Vielfaches gebildet ist.

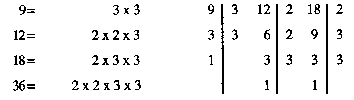
Aus diesem und weiteren Beispielen wird den von der Natur und/oder der bisherigen Umwelt bevorzugten Kindern die Einsicht gelingen, daß zur Bildung des kgV diejenigen Faktoren einer Zahl zu streichen sind, die von der anderen Zahl schon abgedeckt worden sind ...

Diese Strategie läßt sich zusammenfassend in folgendem Stufengang abbilden, in welchem vor allem auch die schwerpunktmäßige Zuwendung des Lehrers zu verschiedenen Kindergruppen deutlich wird:

Der Lehrer spricht wechselweise einmal alle an, dann wieder einzelne Gruppen, wobei die Grenzen ständig im Fluß bleiben. Die Zugehörigkeit zu einer Leistungsgruppe wird nicht durch externe Klassifikation vorentschieden, sondern angesichts der jeweiligen Aufgabe vom Schüler selbst ausgesprochen bzw. durch sein Lernverhalten manifestiert.

2. Wolff-Dietrich Gasztner, der mit seinen traditionellen Hauptschulerfahrungen der heterogenen Zusammensetzung zunächst skeptisch gegenüberstand, wurde schließlich vom Saulus zum Paulus. Als der nach zehnjähriger Erfahrung mit der Inneren Differenzierung von der Behörde gezwungen wurde, Leistungskurse einzuführen, hat er seine Funktion als Abteilungsvorstand zurückgelegt. An dieser Stelle sei sein Modell der in gleicher Weise eleganten wie peniblen Registrierung des individuellen Lernfortschrittes vorgestellt, die ihm als Grundlage und Ausgangspunkt für die je passende Förderung des einzelnen Kindes gedient hat.

Er geht von folgenden Annahmen aus:

W. Gasztner macht sein häufig angewandtes Differenzierungsschema in folgendem Flußdiagramm anschaulich:

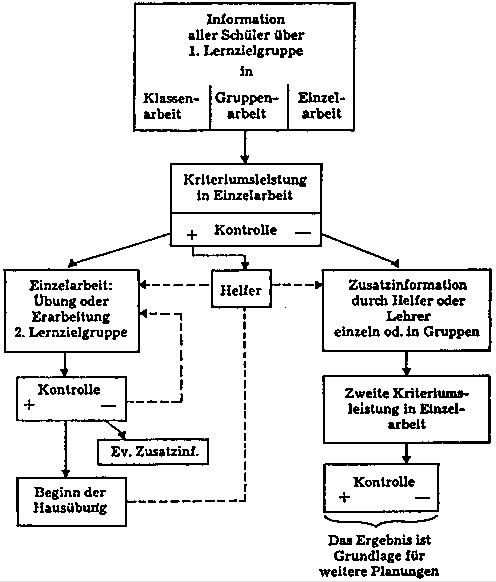
Zur Kontrolle des Lernfortschrittes jedes einzelnen Schülers ist eine Lernzielliste entwickelt worden, die auch der Schüler in die Hand bekommt.

Die Eltern unterschreiben diese Listen und werden auf diese Weise über die Unterrichtsplanung informiert. Es werden pro Jahr fünfmal Lernziellisten ausgegeben. Vier Beispiele aus solchen Lernziellisten sollen verdeutlichen, welche Informationen hier ausgegeben werden.

Seiten im Lehrbuch

Die Buchstaben A, B, C, D geben Bereiche des Mathematikunterrichts an.

A: Mengen und Aussagen

B: Zahlenlehre/Rechnen

C. Größen/Sachrechnen

D: Raumlehre

Die Zahl vor dem Punkt gibt den zeitlichen Abschnitt an. Da es in jedem Schuljahr fünf Abschnitte gibt, bedeutet die Zahl 10, daß dieses Lernziel im letzten Abschnitt der zweiten Klasse angestrebt wird. Trotz dieser zeitlichen Fixierung sind aber Umstellungen durchaus möglich, ohne daß die betroffenen Lernziele neue Nummern erhalten müssen.

Die zweistellige Zahl nach dem Punkt ist die Nummer innerhalb des Abschnittes. Diese Numerierung weist Lücken auf, um jederzeit Ergänzungen vornehmen zu können, ohne das ganze System ändern zu müssen. Fortlaufende Nummern haben nur zusammenhängende Lehrziele. Wenn etwa 01, 02, 03, 04 Nummern von einer solchen zusammenhängenden Lernzielgruppe sind, so belegt die nächste Gruppe die Nummer 10, 11, 12 usf. In den Zwischenraum (05 bis 09) können später weitere Lernziele eingefügt werden.

Selbstverständlich ist auch das Ausstreichen von Lernzielen jederzeit möglich, ohne größere Änderungen zu verursachen. Manche Lernzielnummern sind unterstrichen, andere nicht. Lernziele mit unterstrichener Nummer sollten unbedingt erreicht werden (Fundamentum).

In den Lernziellisten stehen nicht alle Lernziele, die im Laufe von Unterrichtseinheiten erreicht werden sollen, sondern nur solche, die auch noch in größeren Zeitabständen, unter Umständen noch in späteren Schuljahren überprüft werden. Die Erfahrung hat gezeigt, daß die Anzahl der Lernziele von Klasse zu Klasse sinkt (1. Klasse: ca. 10 Maschinschreibseiten; 2. Klasse: ca. 6 Maschinschreibseiten; 3. Klasse: ca. 4 Maschinschreibseiten). Das kommt daher, daß Wiederholungsstoffe, die ja teilweise auch im Lehrplan angegeben sind, nicht noch einmal angegeben werden müssen. Es genügt ein Rückgriff auf die entsprechenden Lernzielnummern eines früheren Schuljahres. - So vorsichtig bei der Erstellung des Fundamentums (unterstrichene Lernzielnummern) vorgegangen wurde, so großzügig wurden Erweiterungsstoffe angeboten. Es darf in keiner Klasse einen Schüler geben, der gegen Ende des Schuljahres keine Ziele mehr vor sich hat. Nicht nur die Unbegabten sollen gefördert, sondern auch die Begabten gefordert werden.

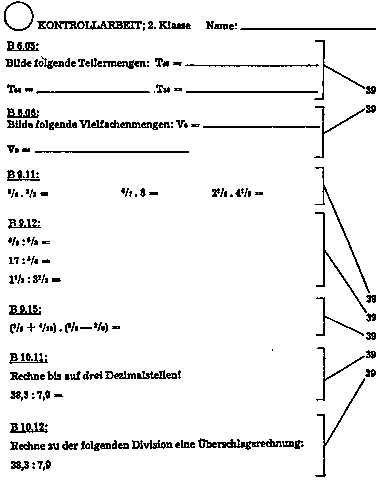
Das Erreichen der Lernziele wird durch verschiedene Maßnahmen kontrolliert: die Möglichkeiten reichen von der Selbstkontrolle durch den Schüler mit Hilfe von Probeaufgaben über das einfache Vergleichen mit einem Lösungsheft mit oder ohne Lehrer und das Besprechen an der Tafel mit ausführlichen Begründungen bis zu lernzielorientierten Tests (Kontrollarbeiten).

Durch eine rationelle Methode der Übertragung der Kontrollarbeitsergebnisse auf die Leistungskarte des Schülers werden nicht nur diese selbst, sondern auch die Schulwoche notiert, in der sie erbracht worden sind. In unserem Beispiel handelt es sich um die 39. Woche.

Zur Markierung der Leistungshöhe werden drei Symbole verwendet, mit denen die Zahl der Schulwoche umschrieben wird. Ein Kreis bedeutet, daß alle Aufgaben einer bestimmten Lernzielnummer richtig sind. Ist nicht alles, aber mehr als die Hälfte richtig, wird ein Viereck um die Zahl 39 gezeichnet: Was darunter liegt, wird mit einem Dreieck versehen:

Nicht beurteilte Aufgaben werden mit einer Klammer eingeschlossen: (39). Durch Nebeneinanderlegen von Kontrollarbeit und Leistungskarte jedes Schülers lassen sich die Ergebnisse zeitsparend auf die Leistungskarte übertragen.

Nach einigen derartigen Kontrollen ergeben die Leistungskarten ein gutes Bild vom Leistungsstand, aber auch von der Entwicklung der Leistung jedes einzelnen Schülers.

Selbstverständlich dürfen die Schüler in ihre Leistungskarte Einblick nehmen. Besonders bewährt hat sich diese Art der Registrierung von Schülerleistungen bei der Elternberatung.

Die Kontrollarbeiten werden mit keiner Gesamtnote versehen, wenngleich dies ohne Schwierigkeit möglich wäre. Das Ummünzen in Noten erfolgt später über Punktwerte. Nach Ablauf von zwei Dritteln eines jeden Semesters werden jedem Schüler sowohl der eigene Zuwachs an Punkten wie auch der Mittelwert und die Extremwerte der Klasse in das Heft eingetragen.

Das Ergebnis der Kontrollarbeiten bildet die Ausgangsbasis für weitere Differenzierungsmaßnahmen. Beispielsweise haben bei der Kontrollarbeit, die in diesem Skriptum wiedergegeben ist, von 28 Schülern sechs die Aufgaben unter dem Lernziel B 9.12 nicht zufriedenstellend gelöst. Auf ihrem Zettel steht neben der Aufgabengruppe ein D und darin 39. Im folgenden Unterricht wurde mit diesen sechs Schülern noch einmal das Dividieren durch Brüche durchgearbeitet, während sich die übrigen Schüler mit anderen Aufgaben beschäftigten.

Das Nacharbeiten in dieser intensiven Art ist aus Zeitgründen natürlich nur bei wichtigen Lernzielen (mit unterstrichenen Nummern) möglich.

Mindestens eine Woche vor der Kontrollarbeit werden die Lernziele bekanntgegeben, die abgeprüft werden können. Viele Schüler arbeiten nach den Lernziellisten die angegebenen Aufgabenarten zu Hause durch und bereiten sich auf diese Weise zielstrebig auf die Kontrollarbeit vor.

Bei jeder Kontrollarbeit werden um zwei Blätter mehr abgezogen, als Schüler in der Klasse sitzen. Eines davon wird mit Lösungen versehen. Nachdem über jeder Aufgabengruppe die Lernzielnummer steht, ist es möglich, die beiden Blätter nach Aufgabengruppen zu zerschneiden und nach Lernzielnummern geordnet auf Karteikarten zu kleben. Jede dieser Karteikarten erhält einen Reiter mit der Lernzielnummer. Der Reiter auf den Karteikarten mit den leeren Zetteln ist gelb, der auf den Karteikarten mit den Lösungen ist rot. Mit der Zeit entsteht auf diese Art eine sehr brauchbare Aufgabensammlung, die für die individuelle Betreuung der Schüler eingesetzt werden kann. Der Lehrer gibt zunächst eine Einzelarbeit. Dann setzt er sich mit den Leistungskarten an den Katheder und betrachtet eine Leistungskarte des Schülers R. Bei Lernziel B 7.01 stehen hintereinander: D und D. Der Schüler hat also dieses Lernziel weder in der 15., noch in der 21. Woche erreicht. Er wird gerufen und erhält aus der Aufgabensammlung eine Karteikarte mit der Lernzielnummer B 7.01 mit gelbem Reiter. Die zweite Karte mit dem roten Reiter wird schief in den Karteikartenbehälter gesteckt, damit sie rasch gefunden werden kann. Auf ähnliche Weise werden noch ungefähr sechs weitere Schüler versorgt, bis der erste Schüler mit seiner Arbeit und der Karteikarte zurückkommt und seine Arbeit zeigt. Die Aufgabenkarte wird mit der Lösungskarte vertauscht. Der Schüler R. hat jetzt richtig gearbeitet. In der Leistungskarte wird mit Bleistift z.B. 7 eingetragen, wenn die Überprüfung in der 7. Schulwoche stattfindet. - Es kommt natürlich vor, daß Schüler abermals falsche Lösungen haben. In diesem Fall muß dem Schüler Hilfe gegeben werden. Je nach Situation kann diese Hilfe durch ein Arbeitsmittel, durch den Lehrer oder einen Schüler gegeben werden.

- ob in der traditionellen Form der Sortierung der Schüler in Gymnasium und zweizügige Hauptschule oder in der quasi-progressiven Form der Sortierung nach der fachspezifischen Fähigkeit in Leistungskurse.

Der Lehrer, der sich für innere Differenzierung interessiert - verantwortliche Pädagogen können dieser Idee nicht entkommen! - möge sich von den elaborierten Systemen des ersten Kapitels nicht abschrecken lassen. Eine Organisationshilfe wie die von Wolff-Dietrich Gasztner entworfene wird ihm ohne Zweifel große Entlastung bringen. Die mikroprozessuale Durchgestaltung einer Unterrichtsstunde wie die vom "kleinsten gemeinsamen Vielfachen" wird aber eher ein seltenes feiertagsdidaktisches Ereignis bleiben müssen. Das möge ihn nicht bekümmern. Wenn die Grundeinstellung stimmt, wenn sich die notwendige Gelassenheit gegenüber dem so unterschiedlichen Fortschreiten der Schüler eingestellt hat und wenn das Informationsmonopol leichten Herzens verabschiedet worden ist, dann ist die wichtigste Voraussetzung für individualisierenden Unterricht bereits geschaffen. Niemand kann ständig gewahr sein, wo jeder einzelne steht. Daß die Schüler partisanengleich ihren geistigen Gefechtsstand besetzt halten und nicht in Reih und Glied marschieren, dies zu akzeptieren ist das eigentlich Neue und gleicht einer kopernikanischen Wende in der Didaktik. Wenn das Wort nicht mißverstanden wird, kann geradezu für eine Art Saloppheit in der methodischen Grundhaltung plädiert werden, weil doch bei entsprechend reizvollem mehrperspektivischen Angebot die Themata selbst zu entsprechender Differenzierung führen. Das Thema "Kinder am Spielplatz" kann einen zukünftigen Breughel faszinieren wie auch den zeichnerischen Stümper. Ähnliches gilt für die sprachliche Ausdrucksschulung und andere Gestaltungsfächer. Was verschiedenen sachkundlichen Informationen von einzelnen Schüler entnommen und von ihm verstanden werden kann, unplanbar und unwägbar. Das häufig angebotene Gespräch wird ihm helfen, in sich stimmige Vorstellungsinhalte auszuformulieren. Lernen kann immer nur jeder für sich selbst! Er wird froh sein, vielfältige Hilfen angeboten zu bekommen; am frohesten aber wird er sein, wenn der Lehrer sein Anderssein nicht nur annimmt, sondern geradezu erwartet.

Für eine Institution der pflichtigen Allgemeinbildung, die diesem Entfaltungsreichtum Raum gibt, ist Selektion ein Fremdwort. Solch eine Schule darf daher klein bleiben und kann in jedem Pfarrdorf errichtet werden, in welchem pro Jahr genügend Kinder geboren werden, um eine einzige Klasse zu füllen. Sie bringt eine regionale Chancenverbesserung zumindest bis zum Ende der Pflichtschulzeit, weil sie gleiche Bedingungen für die Beschickung mit Lehrern wie auch für die Schülerzusammensetzung schafft und an die Abschlußzeugnisse dieselben Berechtigungen knüpft. Vier aufsteigende Klassen der Sekundarstufe 1 binden durch ihr Fachlehrersystem in der Regel sechs Lehrer, sodaß auch für die entsprechende Spezialisierung der Kulturvermittlung gesorgt ist.

Das vielleicht größte Geschenk einer Schule, die auf die Sortierung der Schüler verzichtet und sich der inneren Differenzierung verschreibt, ist, daß die Pflichtschulzeit von Kindern - und Eltern! - noch relativ unbeschwert durchlebt werden kann und das Interesse an der Sache nicht durch unpädagogische Einsprengungen von seiten eines inhumanen Systems gestört wird.

Bernfeld, S.: Sisyphos oder die Grenzen der Erziehung. Frankfurt 1981

Braun/Naudascher: Für eine menschfreundliche Schule. München 1978

Bronfenbrenner, U.: Erziehungssysteme. Kinder in den USA und in der Sowjetunion. Stuttgart 1972

Coleman, J.: Equality of Education Opportunity. Washington 1966

Comenius, J.A.: Große Didaktik. München 1970

Dewey, J.: Demokratie und Erziehung. Braunschweig 1964

Dreikurs/Cassel: Disziplin ohne Strafe. Ravensburg 1979

Fend/Knörzer u.a.: Über Rowdy- und Mogelfaktor, Unordentlichkeit und andere Syndrome. In: Cloer, E.: Disziplinkonflikte in Erziehung und Schule. Bad Heilbrunn 1982, 47-59

Flitner, A.: Konrad, sprach die Frau Mama. Berlin 1982

Gotthelf, J.: Leiden und Freuden eines Schulmeisters. Berlin 1886

Helmke, A.: Schulische Leistungsangst. Frankfurt 1983

Herbart, F.: Kurze Enzyklopädie der Philosophie. Halle 1831

Hoffmann/Rülcker: Lehren und Lernen an Gesamtschulen in Bildungszentren. In: Ztsch. für Pädagogik, 1977, 501-517

Hurrelmann, K.: Unterrichtsorganisation und schulische Sozialisation. Weinheim 1971

Husen, T.: Observations rather than a riplay. In: Oxford Review of Education, Vol. 5, 1979, No. 3, 267-273

Lukesch, H.: Fachspezifische Prüfungsängste. In: Psychologie und Erziehung, 1982, 257-267

Mairinger, B.: Auswirkungen der organisatorischen Maßnahmen des Schulversuchs der 10- bis 14-jährigen auf die sozialen Integration der Schüler. In: Erziehung und Unterricht, 1980, 3, 129-140

Neher, J.: Der Einfluß von Lerngruppenwechsel und Leistungsdifferenzierung auf Bewußtsein und Verhalten von Schülern an einer Integrierten Gesamtschule. In: Die Deutsche Schule, 1981, 10, 596-602

Parsons, T.: Sozialstruktur und Persönlichkeit. Frankfurt 1977

Pfeiffer, I.: Leistungsdifferenzierter Unterricht in der Muttersprache. In: Skowronek/Schmied: Forschungstypen und Forschungsstrategien in der Erziehungswissenschaft. Hamburg 1977, 233-241

Rutter, M.: Fünfzehntausend Stunden. Weinheim 1980

Sandfuchs, U.: Schule als Umwelt des Kindes - aufgezeigt am Problem der Schulgröße. In: Ludwig, H. (Hrsg.): Gesamtschule in der Diskussion. Bad Heilbrunn 1981, 101-115

Vierlinger, R.: Perspektiven einer humanen Schule. Linz 1978

Watzlawick, P.: Menschliche Kommunikation. Bern 1974

Quelle:

Erschienen In: TAFIE (Hrsg.): Pädagogik und Therapie ohne Aussonderung.

5. Gesamtösterreichisches Symposium, S. 25 - 46

Autoreneigenverlag TAK, Innsbruck 1990

bidok - Volltextbibliothek: Wiederveröffentlichung im Internet

Stand: 09.11.2005