"Auf zur Kreativität!" Über das Denken auf unterschiedlichen Schwierigkeits-Stufen
Inhaltsverzeichnis
Für jeden modernen Unterricht, insbesondere für Offenen Unterricht oder für Integrations-Unterricht wird wie selbstverständlich gefordert, daß "Nicht nur die Arbeitsbedingungen, auch die Aufgaben selbst ... offen, d. h. anspruchsvoller werden, Raum für selbständiges Denken und einen inhaltlichen Bezug zu der Erfahrungswelt der Kinder eröffnen."[1]
Nun wird beklagt, daß nur ein Teil der Lehrerschaft dieser Forderung nachkommt. Mögen die Ursachen auch vielfältig sein, mit Sicherheit ist einer der Hauptgründe darin zu suchen, daß die Lehrenden meist darauf angewiesen sind, die Aufgaben allein nach ihrer Erfahrung und gesundem Menschenverstand zu gestalten. So wichtig beide Komponenten sind, die Arbeit würde durch ein Modell erleichtert, welches unterschiedliche Stufen anspruchsvollen oder selbständigen Denkens ausweist. Ein solches Modell will ich darstellen.
Denken als Komplex intern vollzogener Handlungen bildet die Voraussetzung für alle bewußten Lernprozesse. Mit unserer Muttersprache verfügen wir zwar über unterschiedliche Wörter wie "denken", "er-denken", "nach-denken", "vor-denken", "mit-denken", "aus-denken" usw., um verschiedene Arten geistigen Tuns anzudeuten, doch sind die genannten Bezeichnungen wenig geeignet, systematisch bestimmte Denk-Qualitäten zu fördern. Auch bieten sie keine Grundlage, um planvoll verschiedene Schwierigkeits-Stufen des Denkens anzuregen oder um Unterricht nicht nur inhaltlich sondern auch hinsichtlich der Denk-Anforderungen differenzieren zu können.
Das grundlegende Modell der Intern-Operationen wurde von E. KÖNIG und mir schon 1969 mit dem Ziel entwickelt, eindeutige Termini zu gewinnen und eine Grundlage zu schaffen, um
-
planvoll verschiedene Schwierigkeits-Stufen des Denkens anregen,
-
Unterricht nicht nur inhaltlich sondern auch hinsichtlich der Denk-Anforderungen differenzieren,
zu können.
Die Arbeit mit dem Modell zeigte jedoch bald, daß sich mit seiner Hilfe des weiteren folgende Ziele systematisch verfolgen ließen:
-
Lernschwierigkeiten sicherer erkennen und gezieltere Hilfen einsetzen zu können,
-
den Begriff der Kreativität genauer zu fassen und entsprechende Fähigkeiten systematisch aufzubauen,
-
die Lernenden sicherer zur Anwendung des Gelernten zu führen
-
und um Unterricht variabler gestalten zu können (vgl. dazu die Ausführungen im 6. Kap.).
Das Modell bewährte sich in der praktischen Lehre ausgezeichnet, aber aufgrund der strengeren Anforderungen innerhalb der Forschung, insbesondere bei der Konstruktion experimenteller Untersuchungen über den Schwierigkeitsgrad einzelner Intern-Operationen, ergab sich die Notwendigkeit einer Revision des Modells (vgl. dazu Kap. 5 und H. RIEDEL 1990, S. 111-122).
Bild 1 zeigt das revidierte Modell der Intern-Operationen als Baum-Schema, an dessen Zweigspitzen die einzelnen Intern-Operationen angeordnet sind. Das Schema unterscheidet sich gegenüber einer früheren und vorläufigen Fassung (vgl. z. B. RIEDEL 1985, S.101)
-
durch die rigorose Einhaltung der binären Verzweigung
-
und durch die damit verbundene exaktere Unterscheidung der jeweils benachbarten Intern-Operationen.
Das Kriterium, nach dem sich der Baum in Bild 1 verzweigt, ergibt sich aus der Art und Weise, nach welcher die Informationen bei Ausführung der jeweiligen Operation verarbeitet werden.
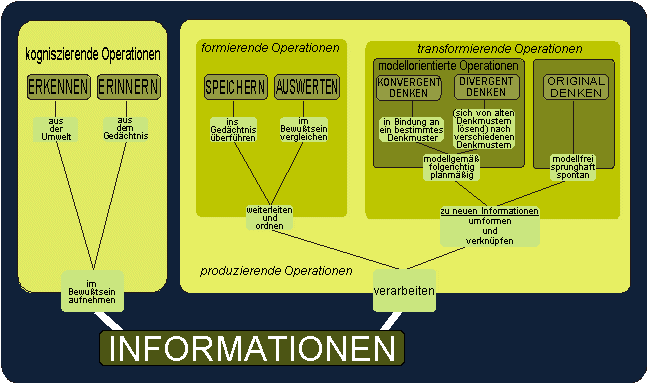
Bild 1: Modell zur Differenzierung von Intern-Operationen (Es wird die Wahl der Vergrößerungs-Stufe 150% zur Betrachtung empfohlen!)
Bevor ich im einzelnen auf die Unterscheidungsmerkmale der Intern-Operationen eingehe, will ich sie zunächst an einem Beispiel zu erläutern versuchen.
Ich beginne dabei mit der kompliziertesten und am wenigsten faßbaren Operation, dem originalen Denken. Daß Künstler beim Erschaffen neuer Kunstprodukte, Techniker bei der Erfindung revolutionierender Instrumentarien und Wissenschaftler beim Entwurf neuer Theorien oft original denken, ist wohl wahr. Aber nur ein geringer Teil der Kunstwerke, Erfindungen und Theorien geht tatsächlich auf originales Denken im Sinne des Bildes 1 zurück, so schöpferisch die Leistungen auch sein mögen. Als schöpferisch oder kreativ sind auch Leistungen zu bezeichnen, die durch andere produzierend-transformierende Operationen zustande kommen, also durch konvergentes oder divergentes Denken.
Welche Intern-Operation für ein bestimmtes Denkergebnis verantwortlich ist, kann nur beurteilt werden, wenn auch der Anfangszustand des Denkenden bekannt ist. Deshalb wähle ich ein Beispiel aus der Wissenschaft, bei dem der Anfangszustand sehr leicht darzustellen ist:
Der als Mathematiker später berühmt gewordene Carl Friedrich Gauß besuchte eine der damals üblichen, wenig-gegliederten Schulen. Schon im 2. Schuljahr fiel der aufgeweckte Schüler dadurch auf, daß er seine Rechenaufgaben stets viel früher als seine Klassenkameraden erledigt hatte und durch Zusatzaufgaben beschäftigt werden mußte.
In einer solchen Situation erteilte der Lehrer dem Schüler Gauß die folgende Aufgabe, um ihn nun für die restliche Unterrichtszeit beschäftigt zu haben: "Zähle alle Zahlen von 1 bis 100 zusammen". Wie groß war das Erstaunen des Lehrers, als Gauß ihm schon nach wenigen Minuten das Ergebnis vorlegte: 5050. Der Lehrer war gezwungen, in mühseliger Rechenarbeit das Ergebnis auf seine Richtigkeit zu überprüfen.
Wie hatte Gauß das Ergebnis so schnell gewinnen können? Es war ihm viel zu umständlich und langweilig gewesen, die langwierigen Ketten von Additionen (1 + 2 + 3 +... bis 100) vorzunehmen. Er vereinfachte die Rechenaufgabe auf völlig neue, noch nie dagewesene Art (die heute in allgemeiner Form als Summen-Formel in der Sekundarstufe gelernt wird). Er sagte sich:
-
1 + 99 ergibt 100, ebenso 2 + 98, 3 + 97, usf.
-
Das geht bis 49 + 51, also 49 mal. 49 x 100 = 4900.
-
Dann fehlen nur noch die 50 und die 100.-
-
Ergibt 5050.
Man kann dem Beispiel entnehmen, daß originales Denken in der Schule nicht planmäßig und systematisch wie andere Intern-Operationen auch ausgebildet werden kann, denn originales Denken geschieht ja gerade nicht nach bisher bekannten Denkmustern, sondern spontan und sprunghaft. Allerdings wurde die Operation auch nicht, wie häufig in ähnlichen Fällen fälschlicherweise geglaubt wird, aus dem Nichts heraus vollzogen, sondern auf der Basis fundierter systematischer Kenntnisse, hier der additiven Beziehungen von Zahlenpaaren, die jeweils 100 ergeben.
Wenden wir unsere Aufmerksamkeit vom "originalen Denken", das in Bild 1 an der äußeren rechten Zweigspitze, also als eine produzierend-transformierende Operation angesiedelt ist, zur gegenüberliegenden Operation auf der linken Seite des Baumes: Erkennen.
Möglicherweise war Ihnen die mathematische Erfindung von Gauß noch unbekannt. Dann hatten Sie Gelegenheit, anhand des letzten Absatzes die Grundidee des Verfahrens zu erkennen: Mit Hilfe der externen Operation "Lesen" entnahmen Sie einem Objekt der Außenwelt, nämlich den letzten Textseiten, eine für Sie neue Information. Diese Information gelangte von außen (wenn auch unter Zuhilfenahme von Gedächtnis-Inhalten) in Ihr Bewußtsein. Würde man das Objekt, an dem Sie operieren konnten (also das Operationsobjekt) so verändern, daß man die einzelnen notwendigen Rechenschritte grafisch und farbig gut gliedert, also die Ergänzungspaare, die Anzahl dieser Paare, die noch nicht erfaßten Zahlen und das Ergebnis, so könnten auch Schüler des 3. oder 4. Schuljahres ohne Schwierigkeit dieselben Informationen erkennen.
Auch bei der in Bild 1 benachbarten Operation, dem Erinnern, ist ein wesentliches Merkmal, daß eine Information ins Bewußtsein transportiert wird. Daher werden beide Operationen auch unter dem Namen "kogneszierende Operationen" zusammengefaßt. Allerdings unterscheiden sich Erkennen und Erinnern in einem wichtigen Punkt: Beim Erkennen entstammt die bewußt werdende Information der Außenwelt. Beim Erinnern ist sie ein Teil des eigenen informations-speichernden Apparates, nämlich des Gedächtnisses. Wenn Sie heute das Summierverfahren von Gauß erkannt haben und es übermorgen einem Freund mitteilen wollen, so müssen Sie alle dann wichtigen Informationen aus Ihrem Gedächtnis ins Bewußtsein heben. Diesen Vorgang bezeichnet die Operation "Erinnern".
Den zwei kogneszierenden Operationen stehen in Bild 1 fünf produzierende Operationen gegenüber. Bevor produzierende Operationen überhaupt ausgeführt werden können, muß mindestens eine kogneszierende Operation realisiert worden sein. Denn produzierende Operationen beinhalten, daß auf die eine oder andere Art bewußt gewordene Informationen weiterverarbeitet werden. Die schwierigste dieser Operationen, das "originale Denken", habe ich anfangs erläutert. Hier geschah die Informationsverarbeitung nicht vorhersehbar, sondern sprunghaft und spontan. Anders dagegen beim konvergenten Denken. Auch mit Hilfe dieser Operation kann man sich völlig neue Kenntnisse erarbeiten.
Nehmen Sie an, Sie würden nach Kenntnis des Gaußschen Summierverfahrens aufgefordert, schnell alle Zahlen von 1 bis 10000 zu addieren. Sie würden dann die einzelnen prinzipiellen Schritte auf den neuen Fall anwenden: Sie würden neue Ergänzungspaare bilden: 1 + 9999, 2 + 9998, 3 + 9997 usw. Sie würden feststellen, daß es 4999 solcher Paare gibt. Sie würden also planmäßig und folgerichtig nach dem schon bekannten Denkmuster von Gauß vorgehen und so schließlich das für Sie noch völlig neue Ergebnis 5.005.000 errechnen.
Konvergentes Denken ,aber auf einem anderen Niveau und bezüglich eines anderen Objekts würde stattfinden, wenn Schüler, die weder das Verfahren noch die Grundidee von Gauß kennen, die Aufgabe erhielten, die Zahlen von 1 bis 100 zu addieren. Mit ihrem Anfangszustand würden sie das ihnen bekannte, aber natürlich umständlichere Verfahren des Addierens (1 + 2 = 3; 3 + 3 = 6; 6 + 4 = 10; ...) so oft folgerichtig und den gelernten Mustern entsprechend anwenden, bis sie als Ergebnis 5050 errechnet hätten.
Anspruchsvoller als das konvergente ist das divergente Denken.
Völlig anders ist die Situation, wenn Schülern mit gleichem Anfangszustand die Aufgabe erteilt würde, lediglich die Zahlen 1 bis 30 "zusammenzuzählen", ihnen aber zusätzlich aufgetragen wird, sich (möglichst viele) verschiedene Möglichkeiten auszudenken, wie die Aufgabe (evtl. schneller oder geschickter) gelöst werden könnte. Wenn ein Schüler dann z.B. auf alle der folgenden Ideen kommt, so vollbringt er bereits eine dem konvergenten Denken überlegene Leistung, er hat dann divergent gedacht:
-
Ich zähle die Zahlen nacheinander zusammen: 1 + 2 = 3; 3 + 3 = 6; ... usw. bis 30.
-
Ich schreibe die Zahlen alle untereinander, dann zähle ich alle Einer zusammen, anschließend dann die Zehner. Schließlich zähle ich die beiden Ergebnisse zusammen.
-
Ich schreibe die Zahlen alle untereinander und rechne "schriftlich".
-
Ich mache drei "Unteraufgaben": Zahlen von 1 bis 10, Zahlen von 11 bis 20, Zahlen von 21 bis 30. Die Zahlen von 1 bis 10 ergeben 55. In den beiden letzten Unteraufgaben ist die erste Aufgabe enthalten. Dazu kommen noch 10mal die 10 und 10mal die 20, also 200 + 100 + 55 + 55 + 55.
-
Ich schreibe wie in d) die Teilmengen nebeneinander. Ich kann rechnen: 3mal kommt die 1 vor, 3mal die 2, 3mal die 3, so weiter bis 9. Dann kommen noch je 1mal die 10, die 20 und die 30. Ich rechne: 3 x 1 = 3; 3 x 2 = 6; 3 x 3 = 9 usw. bis 3 x 9 = 27. Schließlich addiere ich alle Ergebnisse.
Dieser Schüler hat zwar keine so sensationelle Lösung gefunden wie Gauß, aber seine Leistung unterscheidet sich doch bereits vom konvergenten Denken durch ein sehr wichtiges, auch "kreatives" Merkmal: Der Schüler muß sich jedesmal von dem zuvor angewendeten Denkmuster lösen. Er betrachtet das Aufgabenmaterial nach jeweils anderen und immer wieder neuen Gesichtspunkten und entwickelt so verschiedene Lösungsmuster. Diese Art des Denkens wird als "divergentes Denken " bezeichnet.
Das gewählte Beispiel genügt noch nicht, um alle wesentlichen Aspekte der drei transformierenden Operationen (konvergentes Denken, divergentes Denken, originales Denken) deutlich werden zu lassen. Es zeigt aber bereits wesentliche Unterschiede:
Konvergentes Denken und divergentes Denken haben gemeinsam, daß die Informationen folgerichtig und planmäßig sowie auf der Grundlage schon vorhandener Denkmuster verarbeitet werden. Sie werden deshalb als "modell-orientierte Operationen" bezeichnet.
Beim divergenten Denken allerdings genügt nicht wie beim konvergenten Denken das Verarbeiten der Informationen nach nur einem Modell. Vielmehr erfordert es, daß sich der Denkende von einem oder mehreren schon verwendeten Denkmustern zu lösen vermag, um nochmals nach neuen Aspekten und Denkmöglichkeiten zu suchen.
Die dritte transformierende Operation, das originale Denken, dagegen verläuft nicht mehr modellhaft und folgerichtig, sondern sprunghaft, spontan und originell.
Die drei Operationen des konvergenten, divergenten und originalen Denkens haben gemeinsam, daß Informationen umgeformt und auf bestimmte Weise miteinander verknüpft werden, um neue Denkergebnisse zu erzeugen. Sie werden daher unter der Bezeichnung "transformierende Operationen" zusammengefaßt.
Den transformierenden Operationen stehen in Bild 1 die "formierenden Operationen" gegenüber. Sie verlangen nicht, daß Informationen umgeformt und miteinander verknüpft werden, sondern lediglich, daß sie in bestimmter Weise weitergeleitet und geordnet werden.
Beim Auswerten geschieht dies so, daß zwei (oder ggf. mehrere) Informationen ins Bewußtsein genommen, dann aber miteinander verglichen werden. Durch dieses Vergleichen werden Unterschiede, Entsprechungen und Übereinstimmungen festgestellt. Im wesentlichen geschieht dies dadurch, daß die jeweiligen Informationsteile "nebeneinander" gestellt und auf Entsprechung überprüft werden.
-
Um bei dem gewählten Beispiel zu bleiben: Die folgende Aufgabe würde einem Schüler im wesentlichen das Auswerten abverlangen: Es geht wiederum um Summierung der Zahlen von 1 bis 30.
-
Dazu werden aber die Rechenwege a, b und e des o. g. Beispiels zum divergenten Denken vorgegeben, doch zusätzlich noch eine Rechnung, die sich durch eine falsche Anwendung des Verfahrens ergibt.
-
Der Schüler wird aufgefordert, jeden richtigen Lösungsweg zu bestimmen und zu begründen, welchen er vorziehen würde. Hier muß er die einzelnen Lösungsschritte der verschiedenen Verfahren erkennen, dann aber einander gegenüberstellen und sie nach Gesichtspunkten wie Sicherheit, Schwierigkeit und Schnelligkeit vergleichen.
Der Zweck des Informationstransports besteht beim Auswerten also darin, daß ein Vergleich mehrerer Informationseinheiten im Bewußtsein erfolgt.
Ziel des Speicherns [2] dagegen ist der Transport von Informationen durch die Zeit. Aufgrund der relativ kurzen "Gegenwartsdauer" der Informationen im Bewußtsein müssen Informationen, die über lange Zeit aufbewahrt werden sollen, in einen anderen Funktionskomplex, ins Gedächtnis überführt werden.
Das weiß jeder spätestens von jenem Zeitpunkt an, zu dem er erstmals etwas "auswendig lernen" sollte: ein Gedicht, ein Lied, Vokabeln, einen Lehrsatz, grafische Zeichen.
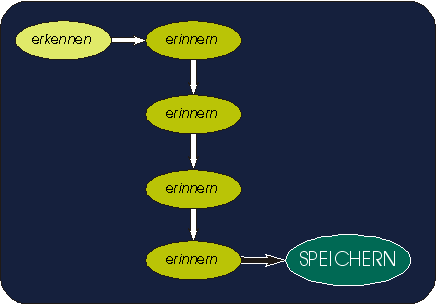
Bild 2: Speichern durch Wiederholen
Obwohl es verschiedene Modellvorstellungen darüber gibt, wie das Abspeichern von Informationen erfolgt, wird trotz umfangreicher Literatur zum "Lernen" und "Üben" im Unterricht meist lediglich ein einziger und daher beim Schüler unbeliebter Weg gewählt: das "Wiederholen" oder "Pauken". Wiederholen ist nichts anderes als mehrfaches Erkennen bzw. Erinnern ein und derselben Information (s. Bild 2). Daß auch dieses übliche, aber trübsinnige, weil langweilige Verfahren zum Erfolg führt, hat folgende Ursachen:
-
Nur etwa 3 Prozent von dem, was uns bewußt ist, können wir für einen längeren Zeitraum als einen Tag abspeichern.[3]
-
Durch die Wiederholung aber wird der Zeitraum vervielfacht, innerhalb dessen die Information bewußt ist. Dementsprechend wächst auch die Wahrscheinlichkeit, daß das Erkannte im Gedächtnis aufgenommen, also gespeichert wird.
Die allerdings beim Wiederholen auftretende Langeweile kommt dadurch zustande, daß die zu leistenden Operationen (Erkennen und Erinnern) lediglich kogneszierender Art sind, den Lernenden geistig also am wenigsten beanspruchen und damit auch am wenigsten interessieren.
In Kenntnis der verschiedenen Intern-Operationen läßt sich der gewünschte Zweck, den Zeitraum zu dehnen, innerhalb dessen die abzuspeichernden Informationen bewußt sind, jedoch auch auf eine andere, den Lernenden stärker beanspruchende und eher motivierende Weise erreichen: durch eine Serie von Situationen, die das auswertende, das konvergent denkende und das divergent denkende Anwenden der erkannten Informationen verlangen.
Bleiben wir bei unserem Beispiel und gehen davon aus, daß ein Schüler das Verfahren von Gauß z.B. am Fall n = 100 erlernt hat.
-
Der scheinbar nächstliegende Weg besteht darin, den Schüler das erlernte Verfahren konvergent denkend anwenden zu lassen. Er soll Zahlen von 1 bis 1000 oder von 1 bis 10, später auch von 1 bis 24 nach dem erlernten Verfahren zusammenrechnen.
-
Gerade für Schüler, denen die Anwendung des Verfahrens noch gewisse Schwierigkeiten bereitet, wären zunächst andere, leichtere Aufgaben angemessen, die nur das auswertende Anwenden des Verfahrens verlangen: Dem Schüler werden fertige Rechnungen vorgelegt, die das Verfahren von Gauß teilweise richtig, teilweise fehlerhaft anwenden. Dabei sollten nicht die arithmetischen Operationen, sondern lediglich die einzelnen Verfahrensschritte falsch oder mangelhaft sein, denn nicht das Rechnen an sich soll produzierend angewendet werden, sondern der neue Rechenweg.
-
Eine weitere Möglichkeit stellt das divergent denkende Anwenden dar. Es ist aber weitaus schwieriger und wird nicht in allen Fällen von jedem Schüler zu leisten sein. Nehmen wir an, er hat das Verfahren am Fall 1 bis 100 kennengelernt. Er soll sich nun neue Aufgabensituationen ausdenken, in denen dieses Verfahren nutzbringend angewendet werden kann. (Möglicher Anreiz: anderen Schülern neue Aufgaben zu stellen). Manche Schüler werden dabei lediglich im Bereich des konvergenten Denkens verbleiben (Zahlen 1 bis 1000, Zahlen 1 bis 10000 usf.), jedoch ließe sich das Verfahren ja auch auf andere (weniger naheliegende Fälle) anwenden: beliebige gerade Zahlenwerte für n, ungerade Zahlenwerte für n, Zahlenreihendie nicht bei 1 beginnen, aus der gegebenen Summe auf die höchste Zahl n zurückrechnen ....
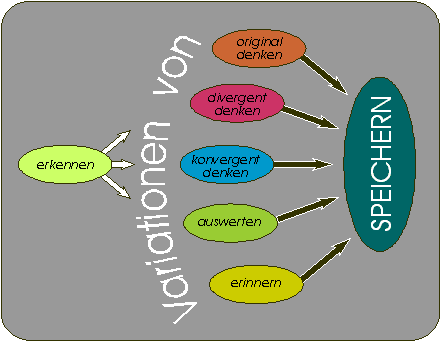
Bild 3: Der Beitrag verschiedener Operationen zum Speicherungs-Prozeß
Bild 3 zeigt den grundsätzlichen Gedanken: Eine Folge und Variation von Aufgaben dieser drei Typen (bei Schülern mit geringem Anfangszustand zunächst in der Reihenfolge vom Erkennen zum Auswerten, dann zum konvergenten Denken, schließlich zum divergenten Denken) wird mit weitaus größerer Sicherheit als das "Wiederholen" im Sinne von mehrfachem Erkennen und Erinnern zur gewünschten Speicherung führen, vermeidet aber die beklagte Eintönigkeit und Langeweile. Das schließt gelegentliche Phasen des Erinnerns nicht aus. Verstärkt wird die Speicher-Wirkung natürlich durch mehrfaches unterschiedliches produzierendes Anwenden. (Der mögliche Einfluß originalen Denkens, das vom Lehrenden nicht direkt initiiert werden kann, ist in Bild 3 nur der Vollständigkeit halber aufgeführt.) [4]
Als weiterer Vorzug dieser Vorgehensweise gegenüber dem Wiederholen im Sinne des Bildes 2 läßt sich voraussagen, daß die Schüler weitaus sicherer und "flexibler" im Umgang mit dem Erlernten sein werden.
[2] Der aufmerksame Betrachter des Modells in Bild 1 wird möglicherweise kritisieren, daß das Speichern gerade wegen der soeben dargestellten didaktischen Wege, eine Speicher-Wirkung zu erzeugen, nicht auf einer Ebene mit anderen produzierenden Operationen dargestellt werden sollte. Denn die Wirkung wird ja durch andere Intern-Operationen erzeugt. Andererseits soll das Modell nicht nur dazu verwendet werden, geistige Handlungen zu beschreiben oder zu veranlassen, die der Lernende an einem Operations-Objekt vornehmen kann, sondern auch welche Fähigkeits-Stufe er durch den Unterricht bezüglich des zu lernenden Unterrichts-Objekts erreicht hat. Unter diesem Aspekt erscheint Speichern der Vereinfachung wegen in der Grafik. S. dazu H. RIEDEL 1992b und 1992c.
[3] Vgl. dazu RIEDEL, H.: Psychostruktur 1967
[4] Weitere sehr wirksame Möglichkeiten der Variation von Aufgaben ergeben sich durch die Steigerung der Konkretions-Stufe und durch den Einsatz von Transformationen. Vgl. dazu H. RIEDEL 1996 und http://bidok.uibk.ac.at/library/riedel-objekte.html.
Ich habe versucht, an nur einem Beispiel die wesentlichen Merkmale der verschiedenen Intern-Operationen zu veranschaulichen. Dabei habe ich in Kauf genommen, daß einige der Beispiel-Variationen etwas künstlich erscheinen mögen. Ich will deshalb in einem zweiten Schritt zunächst die jeweils kennzeichnenden Merkmale der einzelnen Intern-Operationen zusammenfassen und einige andere Beispiele zu ihrer Erläuterung und Klärung anfügen, die zum größten Teil den Publikationen KÖNIG/RIEDEL 1975 und RIEDEL 1979 entstammen.
Intern-Operationen sind (Denk-)Handlungen, durch die vorwiegend Informationen umgesetzt werden (im Gegensatz zu Extern-Operationen, bei denen vorwiegend Energie umgesetzt wird).
Auf einer ersten Ebene werden Intern-Operationen in kogneszierende und produzierende Operationen unterschieden.
-
Durch kogneszierende Operationen werden Informationen lediglich im Bewußtsein aufgenommen. Sie sind Voraussetzung für alle anderen Operationen.
-
Produzierende Operationen zeichnen sich hingegen dadurch aus, daß Informationen weiterverarbeitet werden.
Je nach der Quelle, von der her die ins Bewußtsein gelangenden Informationen stammen, werden zwei kogneszierende Operationen unterschieden:
-
Beim Erkennen entstammen die Informationen der Umwelt. Die Signale der Außenwelt werden durch die Rezeptoren verschlüsselt und im Bewußtsein aufgenommen.
Beispiele:
- Der Inhalt eines Lesetextes wird "verstanden".
- Die Abhängigkeit des Ohm'schen Widerstandes von der Länge des Leiters wird festgestellt.
- Im Musikunterricht wird der Aufbau von Terz und Quart erkannt.
Beim Erinnern entstammen die bewußt werdenden Informationen dem Gedächtnis.
Beispiele:
- Bei der Wahrnehmung eines Verkehrszeichens wird die damit als feste Zuordnung gelernte Bedeutung des Zeichens bewußt.
- Bei der Rechenarbeit erinnert sich der Schüler eines schon früher verwendeten Lösungsweges.
- Nach einer gestrigen Betriebsbesichtigung tragen Schüler in einem Unterrichtsgespräch einzelne Aussagen von interviewten Arbeitern und Angestellten zusammen.
Auf einer zweiten Ebene werden die produzierenden Operationen je nach Art der Informationsverarbeitung unterschieden:
-
Durch die transformierenden Operationen werden die bewußt gewordenen Informationen umgeformt und miteinander verknüpft, so daß neue Informationen erzeugt werden.
-
Durch die formierenden Operationen erfahren die bewußt gewordenen Informationen keine so wesentlichen Veränderungen wie durch die transformierenden Operationen. Sie werden geordnet und weitergeleitet.
Je nach Zweck und Ergebnis des Transports werden die formierenden Operationen zweifach unterschieden:
-
Zweck des Speicherns ist es, die bewußt gewordenen Informationen ins Gedächtnis zu transportieren und dort für längere Zeiträume aufzubewahren. Dabei werden sie schon gespeicherten Informationskomplexen zugeordnet, ohne daß dies in jedem Fall bewußt werden muß.
Beispiele:
- Ein Gedicht wird auswendig gelernt.
- Ein "gefahrloser" Schulweg wird erst zu Fuß zurückgelegt, dann in eine Bildkarte eingezeichnet, dann mündlich dargestellt , wieder gegangen, aus anderen möglichen herausgesucht und begründet, bis er ins Gedächtnis aufgenommen ist.
- Ein Verfahren zur Berechnung von Integralen wird gespeichert.
-
Beim Auswerten werden die Informationen im Bewußtsein "hin-und-hergeschoben", damit sie verglichen, also auf gegenseitige Entsprechungen bzw. Unterschiede hin untersucht werden können. Das Ordnen geschieht hierbei immer bewußt.
Beispiele:
- Schüler bewerten Zeitereignisse unter Heranziehung von Aussagen des Grundgesetzes zur Gleichberechtigung.
- Die Eigenschaften verschiedener Synthetikfasern werden verglichen.
- Lernende finden durch Vergleich verschiedener Geschichtsquellen zur "Kristallnacht" Gemeinsamkeiten der Geschehnisse.
Die transformierenden Operationen werden danach unterschieden, ob die Umformung der Informationen nach bestimmten Mustern oder Modellen erfolgt oder nicht:
-
Durch originales Denken werden die bewußt gewordenen Informationen spontan, sprunghaft und originell zu neuen Ergebnissen verarbeitet, ohne daß auf der Grundlage schon bekannter Muster gedacht wird. (Gauß hatte kein Modell zur Verfügung, von dem her er den neuen Lösungsweg ableiten konnte).
-
Dagegen werden die bewußt gewordenen Informationen durch die modellorientierten Operationen nach bekannten Mustern oder Modellen folgerichtig und planmäßig zu neuen Ergebnissen weiterverarbeitet.
Die modellorientierten Operationen werden ihrerseits zusätzlich nach dem Grad der Fixierung an ein bestimmtes Muster unterschieden:
-
Beim konvergenten Denken erfolgt die Verarbeitung der bewußten Informationen nach einem einzigen Denkmuster, das gewöhnlich zur Lösung dieser oder ähnlicher Problemsituationen angewendet wird.
Beispiele:
- Im bildnerischen Gestalten soll ein Wald mit verschiedenen Grüntönen unter Verwendung der Farben gelb und blau gemalt werden.
- Schüler sollen die "Schärfungs-Regel" auf neue Wörter mit einem S-Laut im Wortinneren anwenden.
- Am Beispiel der Werte 3, 7, 12, 18 , ...wurde das Prinzip einer geometrischen Reihe erkannt. Die Schüler sollen eine andere Reihe auf der Grundlage des Multiplizierens aufstellen.
-
Divergentes Denken dagegen verlangt mehr. Hat der Denkende die bewußt gewordenen Informationen zunächst nach einem ersten Muster verarbeitet, so muß er wieder an den Ausgangspunkt zurückkehren, nach neuen Merkmalen der Problemsituation suchen, sich von dem alten Denkmuster lösen, um nach jeweils neuen Denkmustern zu einem Ergebnis zu kommen versuchen.
Beispiele:
- Der Lernende soll zu einem vorgegebenen musikalischen Thema möglichst verschiedene Variationen finden.
- Im Werkunterricht sollen die unterschiedlichsten Anwendungsmöglichkeiten für den Werkstoff Glas erdacht werden.
- Eine Geschichte wird vorgelesen, kurz vor dem Ende aber abgebrochen. Jeder Schüler soll mindestens drei unterschiedliche Fortsetzungen schreiben.
Meiner Erfahrung nach gibt es zu Beginn des Umgangs mit dem Modell der Intern-Operationen oft Schwierigkeit mit der Unterscheidung des divergenten und des konvergenten Denkens. Deshalb ein weiteres Beispiel hierzu:
Nehmen wir an, Schüler haben im vorangegangenen Unterricht gelernt, daß der Urvogel (Archäopteryx) bereits eine perfekte Befiederung ausgebildet hatte und auch bereits flugfähig gewesen sein muß. Nun muß der Urvogel ja aber einen Vorläufer gehabt haben. Die Lernenden folgern, daß dieser (hypothetische) Vorvogel (Proavis) ebenfalls schon Federn in irgendeiner Form gehabt haben muß, obwohl er noch nicht fliegen konnte. Es erhebt sich nun die spannende Frage nach der ursprünglichen Funktion dieser Federn.
-
Stellt ein Schüler lediglich die Hypothese auf, daß die Vorläufer bereits warmblütig waren und ein Federkleid als Kälteschutz besaßen, so kann man davon ausgehen, daß diese Leistung durch (lediglich) konvergentes Denken zustande gekommen ist. Er hat von seinem bisherigen Wissen ausgehend konsequent in dieser Richtung weitergedacht und eine Lösung gefunden.
-
Ein anderer Schüler entwickelt aber mehrere unterschiedliche Ideen:
- der Vorvogel war wechselwarm und benutzte die Federn als Hitzeschild gegen zu starke Sonneneinstrahlung,
- oder: die befiederten Vorderarme wurden zum Imponieren und Kämpfen verwendet
- oder zum Insektenfang
- oder die Flügel wurden als eine Art Baldachin verwendet, um Wasserreflexe bei der Nahrungssuche am Strand abzuschirmen
- oder die Befiederung hatte eine wasserabstoßende Wirkung.
Dieser Schüler dürfte divergent gedacht haben. Denn er begnügte sich nicht mit einer Lösung. Er hat sich vor jeder neuen Hypothese von seinem bisherigen Gedankengang lösen müssen und in neue Richtungen denken müssen.
Das Beispiel zeigt übrigens deutlich, daß Voraussetzung für diese Leistung eine breitere bzw. differenzierte sog. "Wissens-Basis" ist, als sie der erste Schüler besitzen mußte.
Oft begegnet man dem Argument, daß divergentes Denken im Unterricht nur sehr schwierig anzuregen ist. Das Beispiel zeigt hingegen, daß jeder problem-gesteuerte Unterricht mit der Phase der (selbständigen) Hypothesenbildung sehr gute Möglichkeiten zur Initiation des divergenten Denkens bietet, sofern die Phase nicht - wie meist üblich - im gesamten Klassenverband, sondern in Einzelarbeit oder in kleinen Gruppen realisiert wird. [5]
|
Definitions-Merkmale |
Intern-Operationen |
|
Erkennen |
Von Sinnes-Organen stammende Informationen im Bewußtsein aufnehmen |
|
Erinnern |
Gedächtnis-Inhalte im Bewußtsein aufnehmen |
|
Speichern |
Bewußtseins-Inhalte im Gedächtnis bewahren |
|
Auswerten |
Mehrere Bewußtseins-Inhalte auf Identität oder Entsprechung vergleichen |
|
Konvergent Denken |
Bewußtseins-Inhalte in Bindung an ein bestimmtes Denkmuster neu verknüpfen |
|
Divergent Denken |
Bewußtseins-Inhalte (sich von einem bestimmten Denkmuster lösend) nach verschiedenen Denkmuster neu verknüpfen |
|
Original Denken |
Bewußtseins-Inhalte modellfrei und spontan neu verknüpfen |
[5] Im Klassenverband erhalten nur wenige Schüler die Gelegenheit zum divergenten Denken. Die übrigen können zwar noch produzierende Operationen ausführen, meistens aber werden sie lediglich die Ergebnisse des divergenten Denkens auswerten können. Zur Stellung des problem-gesteuerten Unterrichts s. H. RIEDEL 1990, S. 111
Inhaltsverzeichnis
Die bisherigen Beispiele zur Verdeutlichung der Intern-Operationen entstammen unterschiedlichen Sachbereichen. Um es dem Leser zu erleichtern, die unterschiedlichen Merkmale der für Unterrichtsprozesse besonders wichtigen produzierenden Operationen genauer zu erfassen, füge ich nun Beispiele an, in denen Anwendungen auf der auswertenden, konvergent denkenden und divergent denkenden Stufe am jeweils gleichen Unterrichtsobjekt konkretisiert werden. Gleichzeitig hoffe ich mit der Vielfalt der Beispiele und der Unterschiedlichkeit der Lernbereiche dem immer wieder geäußerten Vorurteil begegnen zu können, daß sich einige Operationen nur in bestimmten Sachgebieten oder Lernbereichen verwirklichen lassen, in anderen dagegen nicht.
Die Schüler haben im vorangegangenen Unterricht einige kennzeichnende Merkmale der Gattung "Märchen" erkannt (dreifache Wiederholung von Situationen, Begegnung von Irdischen mit Über- und Unterirdischen, Verwendung gewisser sprachlicher Formeln wie "Es war einmal").
-
Auswertendes Anwenden: Den Schülern werden kurze Texte und Textausschnitte vorgelegt, die aus Märchen, Sagen und anderen phantastischen Geschichten stammen. Die Schüler sollen jene Textausschnitte herausfinden, die aus Märchen entnommen sind.
-
Konvergent denkendes Anwenden: Die Schüler sollen ein Märchen erdenken, indem sie einige oder auch alle erlernten Klassenmerkmale konkretisieren.
-
Divergent denkendes Anwenden: Die Schüler sollen unter Verwendung der erkannten Klassenmerkmale vier sich im Inhalt möglichst stark unterscheidende Märchen ausdenken. Das Kriterium des Divergenten ist erfüllt, wenn etwa die Dreimaligkeit der Ereignisse durch Variation der Handlungsebene und sehr andersartige Menschen, Tiere, Über- und Unterirdische konkretisiert wird.
Die Lernenden haben zuvor mehrere Verfahren zur Darstellung räumlicher Tiefe bei Bildern erkannt ( - je entfernter, desto weniger farbig, desto grauer, - je entfernter, desto weniger Kontrast, - je näher, desto hellere und dunklere Farben, - je näher, desto präzisere Ausführung, je entfernter, desto weichere undeutlichere Formen - je entfernter, desto "kältere" Farben).
-
Auswertendes Anwenden: Den Schülern werden verschiedene Bilder vorgelegt, in denen die einzelnen Verfahren nicht, teilweise oder vollständig realisiert wurden. Die Schüler sollen unter den erlernten Gesichtspunkten die besseren und schlechteren Bilder herausfinden und ihre Entscheidung begründen.
-
Konvergent denkendes Anwenden: Die Schüler erhalten den Auftrag, zu dem Thema "Dorf inmitten blühender Rapsfelder" Verwendung der gelernten Verfahren ein Bild mit Wasserfarben zu gestalten.
-
Divergent denkendes Anwenden: Die Lernenden sollen möglichst viele Situationen und thematische Anwendungsmöglichkeiten ausdenken und ausführen, in denen die gelernten Verfahren zur Darstellung räumlicher Tiefe sinnvoll eingesetzt werden können. Erst anschließend sollen Bilder realisiert werden.
Die Schüler haben folgenden Versuch durchgeführt: Eine Eisenkugel, die bei Raumtemperatur durch einen vorgegebenen Ring paßt, wird erhitzt, läßt sich nun nicht mehr durch den Ring zwängen, paßt aber nach Abkühlung wieder durch den Ring.
-
Auswertendes Anwenden: Den Schülern werden vier Materialgruppen vorgelegt: Die Werkstücke sind 1. voneinander isoliert und 2. bereits an- und ineinandergefügt. Die Schüler sollen jeweils entscheiden, welches der Werkstücke erhitzt und/oder abgekühlt werden mußte, damit die Werkstücke zusammengefügt werden konnten.
-
Konvergent denkendes Anwenden: Den Schülern werden folgende Materialien vorgegeben: eine Stahlachse, ein darauf leicht drehbares Rad, zwei Kupferrohr-Stücke, deren Innendurchmesser so beschaffen ist, daß sich die Kupferstücke gerade nicht mehr auf die Stahlachse pressen läßt. Die Schüler sollen das Rad so befestigen, daß es sich einerseits leicht auf der Achse dreht, andererseits nicht von der Achse abrutschen kann (Rad auf die Achse schieben, Kupferrohr-Abschnitte durch Erwärmen dehnen, auf die Achse schieben, durch Abkühlen "aufschrumpfen" lassen).
-
Divergent denkendes Anwenden: Die Schüler sollen möglichst viele unterschiedliche Anwendungsmöglichkeiten der an dem Versuch mit der Eisenkugel erkannten Gesetzmäßigkeit erdenken. (Wie beim vorher gezeigten "Aufschrumpfen" das abgelaufene Rad eines Puppenwagens montieren, als "Zaubertrick" durch Abkühlen einen Kupferstift, der zunächst nicht in eine Eisenhülse paßt, unverrückbar fest in die Hülse hineinbringen, durch langzeitigen Druck aufeinander gepreßte, nicht mehr trennbare Bauteile unterschiedlichen Materials durch Abkühlen und/oder Erwärmen voneinander trennen, ...).
Die Schüler haben erkannt, daß ein Dur-Akkord aus unten-liegender großer und darüber-liegender kleiner Terz, daß dagegen ein Moll-Akkord aus unten-liegender kleiner und darüber-liegender großer Terz gebildet wird.
-
Auswertendes Anwenden: Den Schülern werden Notationen einfacher Melodien in Dur und Moll vorgelegt. Die Schüler sollen die Tonqualität bestimmen und ihre Entscheidung begründen.
-
Konvergent denkendes Anwenden: Den Schülern wird eine einfache Melodie in Dur vorgegeben. Sie sollen sie in Moll umsetzen.
-
Divergent denkendes Anwenden: Die Schüler sollen aus nur fünf festgelegten Tönen und zwei frei wählbaren Tönen möglichst unterschiedliche Melodien der Dur- und Moll-Qualität konstruieren.
Die Schüler haben den Satz des Pythagoras gelernt.
-
Auswertendes Anwenden: Den Schülern werden Dreiecke und Vierecke, die in rechtwinklige Dreiecke zerlegbar sind oder nicht, vorgegeben. Dazu werden fertige Berechnungen einzelner Seiten geliefert. Die Schüler sollen entscheiden, welche Rechnungen vom Verfahren her richtig sind, welche nicht.
-
Konvergent denkendes Anwenden: Den Schülern werden rechtwinklige Dreiecke und Vierecke vorgelegt, die in rechtwinklige Dreiecke zerlegbar sind, wobei jeweils eine Kathete oder die Hypotenuse zu berechnen sind.
-
Divergent denkendes Anwenden: Die Schüler sollen möglichst unterschiedliche Anwendungsfälle für den Satz des Pythagoras ausdenken: Berechnung gleichseitiger und gleichschenkliger Dreiecke, Berechnung von nicht bekannten Seiten in Vierecken oder Vielecken, die in rechtwinklige Dreiecke zerlegbar sind, Berechnung nicht bekannter Seiten in Körpern, die in rechtwinklige Dreiecke zerlegbar sind, Erzeugung rechter Winkel für Spielflächen.
Die fünf ausgewählten Beispiele sollten genügen, um zu zeigen, daß das Modell der Intern-Operationen allgemein-didaktischer Art ist, da sich die wichtigen produzierenden Operationen offensichtlich in sehr unterschiedlichen Lernbereichen realisieren lassen. Leider stehen allgemein-didaktische Theorien in dem Ruf, Gültigkeit zu beanspruchen, ohne jemals eine Überprüfung ihres Wahrheits-Gehalts versucht zu haben.
So werden vielleicht auch wohlwollende Leser dieses Aufsatzes fragen, welchen Bewährungsproben das Modell der Intern-Operationen bisher standgehalten hat. Dabei kann "Bewährung" in zwei Richtungen interpretiert werden.
-
Hat sich das Modell in der Unterrichts-Praxis als wirkungsvoll und nützlich erwiesen? (Praxeologische Bewährung)
-
Sind geeignete Experimente unternommen worden, um den "Wahrheits-Gehalt" (hier der Schwierigkeits-Abstufung) des Modells zu überprüfen? (Theoretische Bewährung) [6]
Hinsichtlich der praxeologischen Bewährung praktischen Einsatz anbelangt, so kann auf eine bereits drei Jahrzehnte lange sehr erfolgreiche Erfahrung im Umgang mit dem Modell an Berliner Grundschulen und Universitäten hingewiesen werden. Studenten, Lehrer und Hochschullehrer, die das Konzept der Systemischen Didaktik auch nur teilweise für den Unterricht verwenden, greifen meistens zuerst auf das Teilmodell der Intern-Operationen zurück. Dies geschieht offensichtlich in dem Bewußtsein, daß es ihnen eine Grundlage für höhere Produktivität und Effektivität ihrer Lehrhandlungen bietet. [7]
Zur Überprüfung des Wahrheits-Gehalts der Stufung haben wir an der TU Berlin zwischen 1984 und 1990 eine Serie unterrichts-wissenschaftlicher Experimente, durchgeführt. Im Mittelpunkt standen Untersuchungen zum Schwierigkeitsgrad des Auswertens gegenüber dem konvergenten Denken, denn gerade von langjährig praktizierenden Lehrern wurde nicht akzeptiert, daß das Auswerten eines Sachverhalts leichter sein sollte als das konvergent-denkende Anwenden desselben. Ihr "gesunder Menschenverstand" widerstand auch den Argumenten, daß
-
Auswerten nur verlangt, zuvor erkannte und/oder gespeicherte Informationen miteinander zu vergleichen, konvergentes Denken dagegen, diese Informationen miteinander konstruktiv zu verknüpfen.
-
Beim Auswerten muß nur eine Entscheidung hinsichtlich der Übereinstimmung vorgegebener Informationen gefällt werden, beim konvergenten Denken dagegen müssen Informationen hergestellt werden, die (für den Lernenden) neu sind.
-
Jede Aufgabe zum Auswerten kann vom Lernenden so reduziert werden, daß er lediglich jeweils zwei Merkmale und/oder Relationen zu vergleichen hat, beim konvergenten Denken dagegen muß er gleichzeitig alle notwendigen Informationen bewußt haben, die zur Produktion der neuen Information notwendig sind. (Vgl. RIEDEL 1985, S. 102)
Demzufolge ist die Vermutung gerechtfertigt, daß Auswerten leichter als konvergentes Denken ist. Dies belegen auch unsere Experimente. Trotz aller Bemühungen, die Hypothese zu widerlegen, bewährte sich unsere Modellvorstellung in den verschiedensten Bereichen: Bei Schülern zwischen dem 1. und dem 10. Schuljahr ebenso wie bei Erwachsenen, und dies bei so unterschiedlichen Unterrichtsobjekten wie "Symmetrie" (in Mathematik), "Dreiklänge/Umkehrungen" (in Musik) und "Magnetismus" (im Technisch-naturwissenschaftlicher Elementarunterricht). [8] In allen Untersuchungen
-
machten die Versuchspersonen weniger Fehler beim Auswerten als beim konvergent denkenden Anwenden eines Objekts
-
oder sie brauchten mehr Zeit beim konvergent denkenden Anwenden
-
oder sie waren überhaupt nicht fähig, eine Information konvergent denkend anzuwenden, während sie dennoch dieselbe Information auswertend anzuwenden vermochten.
Damit entsprechen die Ergebnisse dieser Untersuchungen unseren langjährigen praxeologischen Erfahrungen hinsichtlich des Schwierigkeitsunterschiedes von Intern-Operationen wenigstens an diesem besonders kritischen Punkt des Modells.
Um Mißverständnissen vorzubeugen, muß ich betonen, daß die Schwierigkeitsstufung von Intern-Operationen nur eine von zwei Dimensionen zur Beurteilung einer geistigen Leistung darstellt. Die andere Dimension betrifft die Objekte, auf welche die Intern-Operationen angewendet werden bzw. an denen sie vollzogen werden. Beispiele dazu bieten die Bilder 4 bis 7. Wenn eben festgestellt wurde, daß Auswerten leichter sei als konvergentes Denken, so ist damit gemeint, daß der auswertende Umgang mit einem bestimmten Objekt leichter ist als der konvergent denkende Umgang mit demselben Objekt bzw. mit einem Objekt vergleichbarer Komplexität und Kompliziertheit. Anders ausgedrückt: Obwohl die Operation des konvergenten Denkens schwerer als jene des Auswertens ist, könnte das konvergent denkende Anwenden eines einfacheren Informationsgegenstandes u. U. leichter bewältigt werden als das auswertende Anwenden eines viel komplexeren Sachverhalts. [9]
[6] Zur Unterscheidung von praxeologischer, technologischer und theoretischer Bewährung s. H. RIEDEL 1985d und 1988
[7] Weitere positive unterrichtliche Wirkungen des Modells werden im 6. Kapitel ausgeführt.
[8] Vgl. dazu H. RIEDEL 1985a und 1985b, I. H. RIEDEL, I. BREYER und A. SIEGMUND 1986, H. RIEDEL 1986, I. BREYER und H. RIEDEL 1986.
[9] Zur Differenzierung des Objekt-Bereichs s. H. RIEDEL 1996 und http://bidok.uibk.ac.at/library/riedel-objekte.html
Inhaltsverzeichnis
Der Versuch, die Einsatzmöglichkeiten des Modells für den Entwurf und die Einschätzung von Unterricht vollständig darzustellen, würde den Rahmen dieser Arbeit sprengen. Ich beschränke mich deshalb darauf, einige wichtige Aspekte aufzureihen:
"Auf zur Kreativität" hatte ich diesen Aufsatz plakativ überschrieben. Damit wollte ich einerseits ausdrücken, daß der sehr weiche und verschwommene Begriff der Kreativität genauer gefaßt werden kann. Leicht läßt sich zeigen, daß unterschiedliche Intern-Operationen den Begriff der Kreativität abdecken, je nachdem wie weit der Begriff interpretiert wird.
Mit Sicherheit denkt jemand kreativ, wenn er, wie in unserem Beispiel von der Summierung nach GAUSS original denkt. Doch wie verschiedene Beispiele, besonders jenes vom Archäopteryx andeuten, ist auch divergentes Denken kreatives Denken. Schließlich kann man auch Leistungen, die durch konvergentes Denken erbracht werden, der Kreativität zurechnen.
Denken wir nur an das Beispiel vom "Aufschrumpfen": Der Schüler, der durch Aufschrumpfen der Kupferrohr-Abschnitte ein Rad am Puppenwagen befestigen konnte, hat zwar "nur" konvergent, aber doch in hohem Maße schöpferisch gedacht.
Lehrer freuen sich manchmal auch bereits, wenn ihre Schüler durch Auswerten neue Informationen "selbst entdecken" oder "erforschen".
Man lege ihnen beispielsweise drei Bilder von MIRO, eines von KLEE vor. Sie "entdecken", daß eines der Bilder von einem anderen Maler stammen müßte und daß der Maler der anderen drei Bilder (MIRO) immer wieder kindertümliche Strich-Symbole verwendet. Würden Sie solch ein "selbständiges Entdecken" auch schon als Kreativität werten?
Andererseits sollte aufgezeigt werden, daß die Förderung von Kreativität nicht dem Zufall überlassen bleiben muß. Wie oft mißverstanden wird, reicht das Gewähren von Freiräumen keinesfalls. Zum kreativen Tun können Lernende planvoll und systematisch geführt werden. Neben der Schaffung einer soliden Informations-Grundlage kann dies hervorragend dadurch bewirkt werden, daß die Lernenden schrittweise über das Auswerten und konvergent-denkende Anwenden zum divergent-denkenden Anwenden befähigt werden. Fördert und würdigt der Lehrende ein solchermaßen vorbereitetes divergentes Denken, so kann er die berechtigte Hoffnung hegen, daß ihn seine Lernenden auch mit Ergebnissen originalen Denkens überraschen werden. Daß dies auch entsprechend positiv gewürdigt werden muß, versteht sich von selbst.
Wenn Lehrer von besonders kreativen Schülern schwärmen, so handelt es sich bei jenen oft um Personen, die bereits über eine Vielfalt von Modellen verfügen und diese divergent, oft aber auch nur konvergent einsetzen. Um so größer sind die Enttäuschungen solcher Lehrer, wenn sie nicht den Unterschied zwischen diesen beiden Operationen und dem originalen Denken kennen und deshalb unbewußt eine originale Leistung von den Schülern fordern. [10]
Die Beispiele dürften auch zeigen, daß das Modell der Intern-Operationen eine ausgezeichnete Basis für die Differenzierung des Unterrichts darstellt. Dies trifft sowohl für die Phase des Erkennens als auch für die Phase der Anwendung zu.
Wer an Differenzierung denkt, hat vornehmlich im Sinn, die Aufgaben hinsichtlich ihres Schwierigkeitsgrads zu stufen und somit dem jeweiligen Anfangs-Zustand der Lernenden anpassen zu können. Allerdings bezieht sich die Variierung der Schwierigkeit in der gängigen Praxis fast immer nur auf das Unterrichts-Objekt.
-
Schüler mit hohem Anfangs-Zustand erhalten Aufgaben zum schriftlichen Addieren, bei denen an mehreren Stellen die 10 überschritten wird,
-
Lernende mit mittlerem Anfangs-Zustand solche, bei denen nur einmal genau 10 erreicht wird
-
und Schüler mit geringem Anfangs-Zustand Aufgaben, bei denen der Zehner nie erreicht wird.
Mit Kenntnis des Modells der Intern-Operationen kann auch schon bezüglich derselben Schwierigkeits-Stufe des Unterrichts-Objekts differenziert werden, indem die Lernenden auf unterschiedlichem Schwierigkeitsgrad der Operation gefordert werden.
-
Alle Lernenden erhalten Aufgaben mit Zehner-Überschreitung.
-
Aber einige brauchen nur zwischen vorgelegten falschen und richtigen Rechnungen auswerten,
-
andere müssen das Verfahren konvergent denkend umsetzen, indem sie entsprechende Aufgaben ausrechnen müssen,
-
andere Schüler sollen sich divergent denkend möglichst unterschiedliche Aufgaben hierfür ausdenken, um sie anderen Schülern zu stellen.
Damit wird die Variationsbreite möglicher Schwierigkeits-Stufen um das Mehrfache erweitert. Man kann nun nach dem Unterrichts-Objekt und nach der Intern-Operation differenzieren.
Die Jahrhunderte alte Forderung, Unterricht "vom Leichten zum Schweren" aufzubauen, hat auch für heutigen Unterricht seine Gültigkeit nicht vollständig verloren. Zwar ist sie überholt, wenn Schüler problem-gesteuert oder -entdeckend lernen sollen. Sobald sich aber die Notwendigkeit ergibt, aufgaben-gesteuert oder auch nur nachvollziehend zu lernen [11] , ist der systematische Aufbau von lehrgangsmäßigen Unterrichts-Einheiten oder -Sequenzen von größter Wichtigkeit. Daß dies besonders wirksam entsprechend dem steigenden Schwierigkeitsgrad der Intern-Operationen von links nach rechts in Bild 1 geschehen kann, geht eigentlich schon aus den Ausführungen über Kreativität und Differenzierung hervor. Die tägliche Unterrichts-Praxis zeigt jedoch, daß Lehrende, ohne daß es ihnen hinreichend bewußt ist, gegen diesen Grundsatz verstoßen, weil sie unmittelbar nach einer, wenn auch noch so interessanten und gediegenen Erkennens-Phase, meist als "Einführung" bezeichnet, unmittelbar danach erwarten, daß die Lernenden die gewonnenenen Informationen nun auch konvergent denkend anwenden können.
Sehr oft wird - dem Lehrer unbewußt - gleichzeitig verlangt, daß die zu verarbeitenden Informationen auch schon gespeichert sind:
-
Beispielsweise sollen Schüler im 3. Schuljahr das Verfahren zur schriftlichen Addition konvergent denkend auf neue Fälle anwenden, oder in einer Diplomprüfung wird das konvergent denkende Anwenden von Rechtsvorschriften auf einen konkreten Rechtsfall verlangt. Nach einmaligem Erkennen kann nicht erwartet werden, daß die Lernenden alle Schritte des Rechenverfahrens oder alle Einzelheiten der Rechtsvorschriften erinnern können.
-
Die produzierende Anwendung würde dagegen leichter gelingen, wenn den Lernenden zusätzliche externe Operations-Objekte, beispielsweise das Rechenverfahren in Form von "Merkschritten" oder anhand eines konkreten Beispiels bzw. eine dem Rechtsfall entsprechende Sammlung von Rechtsvorschriften angeboten werden.
Allgemein kann man formulieren: Wegen der nicht beliebig erweiterbaren Bewußtseins-Kapazität muß der Informations-Gehalt des zu verarbeitenden Materials um so geringer sein, je schwieriger die verlangte Intern-Operation ist.
Ein anderer Mangel läßt sich in der gängigen beobachten: da Lehrer oft nicht die Bedeutung der formierenden Operation Auswerten kennen oder ihr nicht genügend Gewicht beimessen, überfordern sie ihre Schüler.
-
So ist ein durchschnittlicher Lehrer-Student fast immer überfordert, wenn er unter Verwendung zuvor gemeinsam als geeignet befundener didaktischer Kriterien erstmals eine Unterrichtseinheit planen soll, die Kriterien also mindestens konvergent, wünschenswerterweise sogar divergent denkend anwenden soll.
-
Gibt man ihm dagegen Gelegenheit, dieselben Kriterien an schon vorhandenen Unterrichts-Aufzeichnungen oder -Planungen auswertend anzuwenden, so hat dies nicht nur den unter motivationellen Gesichtspunkten sehr wesentlichen Effekt, daß er zu einem erfolgreichen Ergebnis gelangt, sondern gleichzeitig werden noch nicht bewußte Schwierigkeiten im Umgang mit den zu verarbeitenden Kriterien abgebaut: Die wesentlichen Merkmale, ihre Wirkungsbreite, ihr Gültigkeitsbereich werden deutlicher. Insgesamt wird der Informations-Gehalt des bearbeiteten Objekts herabgesetzt. Damit wird der Student eher befähigt, anschließend die schwierigere Leistung des konvergent denkenden Anwendens etwa bei der Planung einer neuen Unterrichts-Situation zu erbringen.
Gleiches gilt für Lernende auf allen Schulstufen. Durch die Operation des Auswertens wird in der Regel dreierlei bewirkt:
-
Einerseits werden oft erst alle für produzierende Leistungen wesentlichen Informations-Bestandteile hinreichend bewußt gemacht,
-
andererseits wird durch den Vollzug der produzierenden Operationen auf niedrigem Schwierigkeitsniveau eine Verringerung des subjektiven Informations-Gehalts bewirkt, den das Unterrichts-Objekt für den Lernenden besitzt.
-
Unabhängig hiervon erhält der Lernende (bei hinreichend guten konstruierten Operations-Objekten (im weiteren Sinne: Lern-Materialien) [12] Anregung für den Aspekte-Wechsel, der eine notwendige Voraussetzung für das spätere divergent-denkende Anwenden darstellt.
Lehrende fühlen sich zu Recht sehr oft unter starkem Zeitdruck, wenn sie die Vorgaben des Rahmenplans erfüllen wollen. Das führt leicht dazu, daß der Unterricht zwar noch sorgfältig für die Phase des Erkennens (in der sog. "Einführungs-Phase") geplant wird, daß aber die anschließenden Unterrichts-Abschnitte, die zur Anwendung des Erkannten führen sollen, stark vernachlässigt werden.
Bild 5: Operations-Objekt zum auswertenden Anwenden der "Zwei-Pole-Wirkung des Magneten"
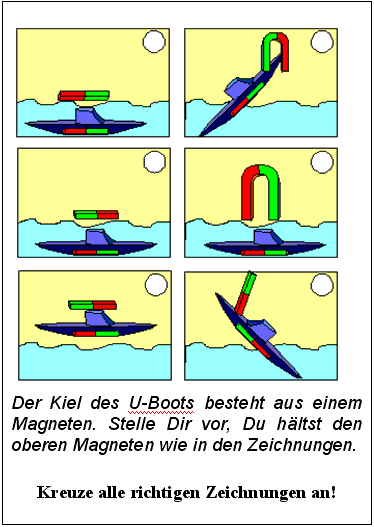
Bild 6: Verändertes Operations-Objekt zum auswertenden Anwenden der "Zwei-Pole-Wirkung des Magneten"
Auch wenn man geneigt ist, formalen Aspekten nicht allzu starkes Gewicht beizumessen, soll hier doch nicht unerwähnt bleiben, daß entsprechende Engpässe eher umgangen werden können, wenn in die Formulierung von "Lernzielen" die Festlegung jener Intern-Operation aufgenommen wird, die am Ende des Unterrichts von den Lernenden erwartet wird. Denn aus der Kennzeichnung der Intern-Operation kann leichter der Bedarf an Lern- und damit auch an Unterrichts-Zeit abgeschätzt werden.
-
Die Formulierung "Zwei-Pole-Wirkung des Magneten" als Lernziel, besagt lediglich, daß Schüler lernen sollen, welche Pole des Magneten sich gegenseitig anziehen oder abstoßen. Es ist jedoch nichts über die geistige Leistung bzw. Fähigkeit der Lernenden ausgesagt, besagte Information in für sie neuen Situationen anzuwenden.
-
Auch die verbreitete Formulierung "Die Lernenden sollen zeigen, daß sich gleichnamige Pole abstoßen und ungleichnamige Pole anziehen" [13] enthält keinen Hinweis darauf, daß die Schüler mehr leisten müssen, als sich nur an Handlungen zu erinnern, die sie im Unterricht bereits vollzogen haben.
Nach dem bisher Ausgeführten kann der Leser leicht nachvollziehen, daß das Hinzufügen einer produzierenden Operation zum Unterrichts-Objekt hier eine deutliche Verbesserung bringt. Das folgende Beispiel entstammt einer experimentellen Untersuchung, die wir an der TU Berlin zur Wirkung problem-gesteuerten Unterrichts durchführten [14].
Die Operations-Objekte sowohl in Bild 5 als auch in Bild 6 verlangen vom Lernenden, daß er die zuvor erkannte Information über die Dipol-Wirkung des Magneten auswertend anwendet (jedenfalls sofern er die Aufgaben nicht schon zuvor bearbeitet hat).
-
Während sich die erste Aufgabe jedoch noch ganz eng an jene labor-artigen Operations-Objekte hält, mit denen der Lernende während der Erkennens-Phase manipulieren konnte, stellt die zweite Aufgabe schon einen Bezug zu einer (für die noch gerne mit ähnlichem Spielzeug umgehenden Schüler) "praktischen" Lebens-Situation her. Die Operations-Objekte unterscheiden sich, nicht aber die vom Lernenden zu leistende Intern-Operation!

Bild 7: Aufgabe zum konvergent-denkenden Anwenden der "Zwei-Pole-Wirkung des Magneten"
-
Das konvergent-denkende Anwenden verlangt andere, aber nicht notwendigerweise aufwendigere Operations-Objekte. Die Aufgabe laut Bild 7 entspricht hinsichtlich des Operations-Objekts in etwa jener des Bildes 5, aber hier werden dem Lernenden nicht wie beim Auswerten neue Situationen vorgegeben, deren Stimmigkeit er ("lediglich") beurteilen muß. Nein, er muß neue Informationen selbst erdenken.
-
Anspruchsvoller wäre das Operations-Objekt laut Bild 8, aber eben gleichfalls zum konvergent-denkenden Anwenden, ebenso aber auch beispielsweise die Aufgabe, einen Magneten in einem Holzgestell "schweben" zu lassen.
Durch die Festlegung der jeweiligen Intern-Operation wird also eine Klasse möglicher Operations-Objekte oder Aufgaben erfaßt, welche die (jedenfalls auf das Unterrichts-Objekt bezogen [15]) gleiche Leistung erfordern.
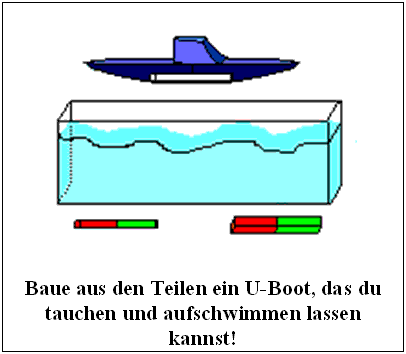
Bild 8: Aufgabe zum konvergent-denkenden Anwenden der "Zwei-Pole-Wirkung des Magneten"
In allen Fällen müssen die Lernenden die zuvor erlernte Information in einer für sie neuen Situation anwenden, einerseits jedoch "nur" auswertend, andererseits dagegen konvergent denkend. Durch entsprechend geplante produzierende Phasen wird dann auch viel wahrscheinlicher, daß Schüler das erlernte Wissen auf praktische Situationen sofort, aber auch später selbständig anwenden können, wie die Beispiele zum U-Boot zeigen.
Verstärkt würde die Wirkung natürlich, wenn die Lernenden auch schon innerhalb der Unterrichts-Einheit zum divergenten Anwenden angehalten würden.
Die Anregung, andere Erfindungen als die bereits bekannten oder erörterten zu machen, mag überzogen erscheinen. Aber auf der Grundlage des durch Auswerten und konvergentes Denken hinreichend "gesicherten" Wissens gelingt es vielen Schülern mancherlei neues zu erfinden, so beispielsweise einen magnetischen Türstopper, eine "schwebendes" Fahrzeug u.a.
Langzeit-Planungen werden mit größerer Sicherheit erstellt werden können, wenn der Lehrende gelernt hat, mit dem Instrumentarium der Intern-Operationen umzugehen. Die Kennzeichnung der Operations-Ziele durch Operationen läßt ihn wenigstens grob den unterrichtlichen Zeitaufwand abschätzen, der für die jeweiligen geistigen Leistungen benötigt wird, ohne daß die Operations-Objekte bereits konkretisiert worden sind.
Den überzeugendsten Eindruck hat meiner Erfahrung nach das Modell der Intern-Operationen bei jenen Lehrern oder angehenden Lehrern hinterlassen, die sich zuvor darum bemüht hatten, besonders leistungs-schwachen Kindern, sei es im Integrations- Unterricht, im Förder-Unterricht, in der individuellen Schulhilfe, oder im Privat-Unterricht eine sichere Ausgangs-Basis für ein künftiges Mit-Lernen im Klassen- oder Gruppenverband zu verschaffen.
Übereinstimmend betonen sie, daß es Ihnen meistens trotz ausgefeilter "Einführungs-Phasen" nicht gelungen war, die Lernenden auf eine Stufe zu bringen, auf welcher sie das Gelernte hätten anwenden sollen. Erst mit Hilfe der Schwierigkeits-Stufung des Denkens, die ihnen durch das Modell der Intern-Operationen deutlich geworden war, gelang es ihnen festzustellen, welche Schwierigkeiten die Schüler (meistens auf der Ebene des konvergenten Denkens) hatten.
Hatten Sie zuvor nur die Möglichkeit gehabt, die Aufgaben zu erleichtern oder zu vereinfachen, indem sie wie im Mathematik-Unterricht die Zahlen-Werte auf reine Zehner, Einer oder Hunderter einengten, oder im Rechtschreib-Unterricht die anzuwendende Regel oder die sie repräsentierenden Fälle reduzierten, oder nochmals richtige Beispiele "gemeinsam" bearbeiteten oder andere hinreichend bekannte Hilfen anboten, die sich durch Veränderung des Operations- oder des Unterrichts-Objekts ergaben, so konnten sie nun unabhängig hiervon oder zusätzlich die von den Lernenden auszuführende Operation vereinfachen.
Erfahrungsgemäß erbrachte allein die Veränderung der Aufgaben in solche zum Auswerten großen Erfolg. Die Erklärung ist einfach: durch das Auswerten nach der Erkennens-Phase wurden den Schülern wichtige Aspekte nochmals bewußt gemacht, auch wo Fehler-Möglichkeiten liegen, vor allem aber wurde die subjektive Information des "Lernstoffs" durch die zwar einfache, aber schon produzierende Operation des Auswertens so reduziert, daß oft schon nach einmaligem Auswerten das konvergent-denkende Anwenden gelang.
Man sollte selbst erleben, welche Freude dies den so oft demotivierten Kindern bereitet!
In Kapitel 2 habe ich bereits darauf hingewiesen, daß sich durch geschickte Reihung und Variation der Anwendungsphasen im Sinne der drei Operationen auswerten, konvergent und divergent denken auf didaktisch elegante und wirkungsvolle Weise eine sichere Speicherung von Unterrichtsobjekten erzielen läßt.
Neben diesem Vorteil und jenem der verstärkten Anwendungs-Fähigkeit ist ein dritter nicht weniger bedeutungsvoll: Der Unterricht, selbst wenn er nicht die Qualität des aufgaben-gesteuerten Lernens überschreitet, wird durch Einsatz der verschiedenen produzierenden Operationen mit Sicherheit abwechslungsreicher für die Lernenden. Denn jede dieser Intern-Operationen verlangt andere Arten von Operations-Objekten, wie dies schon durch die Beispiele zur Dipol-Wirkung angedeutet ist. Dieser Wechsel an geistiger Beanspruchung bewirkt natürlich auch eine nicht unbeträchtliche Motivierung der Lernenden.
Abschließend sei bemerkt, daß üblicher Unterricht durch Kenntnis und Anwendung des ausgeführten Modells sicher in mancherlei Hinsicht verbessert werden kann. Die Tatsache, daß ich das Modell hier aus Gründen der Übersicht und des Verständnisses isoliert von anderen wichtigen Teil-Modellen der Systemischen Didaktik darstelle, birgt aber die Gefahr in sich, daß es in verkürzter Sicht praktiziert werden könnte. Meine Bitte an den gutwilligen Leser: Beschäftigen Sie sich mit anderen Teil-Modellen [16] der Systemischen Didaktik wenigstens in so weit, daß Sie deren Zusammenhänge mit Intern-Operationen erkennen!
[10] Die Höhe ihres Anspruchs bleibt den Lehrenden deshalb verborgen, weil sie selbst die geforderte Leistung entweder durch ("nur") modell-orientierte Operationen erworben, oft aber sogar nur imitativ übernommen haben.
[11] Zur Differenzierung von Lernprozessen hinsichtlich des Grades an Selbständigkeit s. RIEDEL, H. 1998 und http://bidok.uibk.ac.at/library/riedel-selbstaendigkeit.html.
[12] Operations-Objekte sind jene Objekte, die den Lernenden zu den genannten Operationen anregen. Eine Ausführung des Modells findet der Leser in H. RIEDEL 1996 und unter http://bidok.uibk.ac.at/library/riedel-objekte.html
[13] Solche oder ähnliche Formulierungen gehen auf den Einfluß des Behaviouristen R. F. MAGER (1965) zurück und wurden lange Zeit favorisiert, um das Vermögen der Lernenden am Ende des Unterrichts zu kennzeichnen und überprüfbar zu machen. Die sog. "Operationalisierung" des Lernzieles erfolgte also nicht durch Zufügung einer Intern- sondern einer Extern-Operation, die wie anfangs schon gezeigt wurde, ungeeignet ist, die Qualität der verlangten Intern-Operation anzuzeigen.
[14] vgl. I. BREYER, H. RIEDEL, F. REICHARD 1987, S. 124 - 138.
[15] Die unterschiedliche Leistung, die sich zusätzlich aus der Art der Operations-Objekte ergibt, kann mit Hilfe des Modells zur Differenzierung von Operations-Objekten ebenfalls bestimmt werden. Vgl. dazu H. RIEDEL 1996 und http://bidok.uibk.ac.at/library/riedel-objekte.html.
[16] Die wichtigsten Teil-Modelle zu Lernsituationen, Lernprozessen, Operations-Objekten und Grundformen von Unterrichts-Objekten findet der Leser unter http://bidok.uibk.ac.at/texte/riedel-einfuehrung.html
BREYER, H. und I. BREYER: Zum Begriff der Operation in der Systemtheoretischen Didaktik. In: Sachunterricht und Mathematik in der Grundschule. 1975, S. 365 - 370.
BRÜGELMANN, H.: Die Öffnung des Unterrichts muß radikaler gedacht, aber auch klarer strukturiert werden. http/bidok.ac.at/texte/bruegelmann-radikal. 1999
BREYER, I., H. RIEDEL, F. REICHARD: Experiment über die Wirkung von Problemstellungen zu Beginn des Unterrichts. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 1987, S. 124-138.
KÖNIG, E. / RIEDEL, H.: Skizze eines Systems zur sozio-technischen Objektivierung der Planung von Lernsituationen. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 1969, S.85 -98
KÖNIG, E. / RIEDEL, H: Unterrichtsplanung I. Konstruktionsgrundlagen und -kriterien, Beltz, Weinheim und Basel, 1975
MAGER, R. F.: Lernziele und Programmierter Unterricht. Beltz. 1965
RIEDEL, H.: Psychostruktur. Aufbau eines einfachen :Psychostrukturmodells für die algorithmische Lehrprogrammierung. Schnelle, Quickborn 1967
RIEDEL, H.: Zum Standort der Systemtheoretischen Didaktik. In: RIEDEL, H. (Hrsg.): Standort und Anwendung der Systemtheoretischen Didaktik. Kösel, München, 1979
RIEDEL, H.: Vorbereitung eines Experiments zur Schwierigkeitsstufung von Intern-Operationen. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 1985, S. 99-110
RIEDEL, H.: Vorüberlegungen zur Revision des Modells der Intern-Operationen. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 1990. S. 111-122.
RIEDEL; H.: Neufassung eines Modells der Internoperationen. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 1, 32, 1991 a, S. 15-28.
RIEDEL, H.: Das Modell der Intern-Operationen als Baustein in der Systemischen Didaktik. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 3, 33, 1992 b, S. 113-124
RIEDEL, H.: Weitere Beiträge des Modells der Intern-Operationen in der Systemischen Didaktik. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 4, 33 1992 c, S. 151-163
RIEDEL, H.: Poppers Drei-Welten-Theorie und Objekt-Bereiche des Unterrichts. Grundlagensstudien aus Kybernetik und Geisteswissenschaft 35, H. 3, 1994 , S. 114-126
RIEDEL, H.: Systemische Betrachtungen über Operations-Objekte. Deutsche Übersetzung von RIEDEL, H.: Systémová úvaha o operacnyých objektoch. In: POLÁKOVÁ, E. (Hrsg.): Teoretické východiská technológie vzdelávania. Pedagogická fakulta VSPg Nitra. 1996
RIEDEL, H.: Differenzierung von Lernprozessen unter dem Gesichtspunkt der Selbständigkeit TU - WE 0231 Berlin, 1998
Quelle:
Harald Riedel: Ein Modell zur Differenzierung von Intern-Operationen "Auf zur Kreativität!" Über das Denken auf unterschiedlichen Schwierigkeits-Stufen
bidok - Volltextbibliothek: Wiederveröffentlichung im Internet
Stand: 04.10.2006
